Lecture 3 - CS50x 2023
欢迎!
- 在第 0 周,我们介绍了算法的概念。
- 本周,我们将通过伪代码和代码本身来扩展我们对算法的理解。
- 此外,我们将考虑这些算法的效率。实际上,我们将基于上周讨论的一些底层概念,来构建对算法的理解。
算法
回想一下,上周我们介绍了数组的概念,它指的是彼此相邻的内存块。
你可以将数组形象地想象成一排七个红色储物柜,如下图所示:
我们可以想象,我们有一个基本问题,想知道“数字 50 是否在数组中?”
我们可以将数组交给一个算法,该算法会在储物柜中搜索数字 50 是否存在,并返回 true 或 false。
我们可以想象我们可以为我们的算法提供各种指令来执行此任务,如下所示:
对于从左到右的每个门
如果 50 在门后
返回 true
返回 false请注意,上面的指令被称为伪代码:一种人类可读的、可以提供给计算机的指令。
计算机科学家可以将伪代码翻译如下:
对于 i 从 0 到 n-1
如果 50 在 doors[i] 后面
返回 true
返回 false请注意,虽然这还不是代码,但已经非常接近最终代码的形式了。
二分搜索是一种搜索算法,可以用来查找数字 50。
假设储物柜中的值已经按从小到大的顺序排列,那么二分搜索的伪代码如下:
如果没有门
返回 false
如果 50 在中间的门后
返回 true
否则如果 50 < 中间的门
搜索左半部分
否则如果 50 > 中间的门
搜索右半部分使用代码的术语,我们可以进一步修改算法如下:
如果没有门
返回 false
如果 50 在 doors[middle] 后面
返回 true
否则如果 50 < doors[middle]
搜索 doors[0] 到 doors[middle-1]
否则如果 50 > doors[middle]
搜索 doors[middle+1] 到 doors[n-1]请注意,通过这个近似的代码,你几乎可以想象它在实际代码中会是什么样子。
运行时间
运行时间分析涉及到 big O 符号。请看下图:
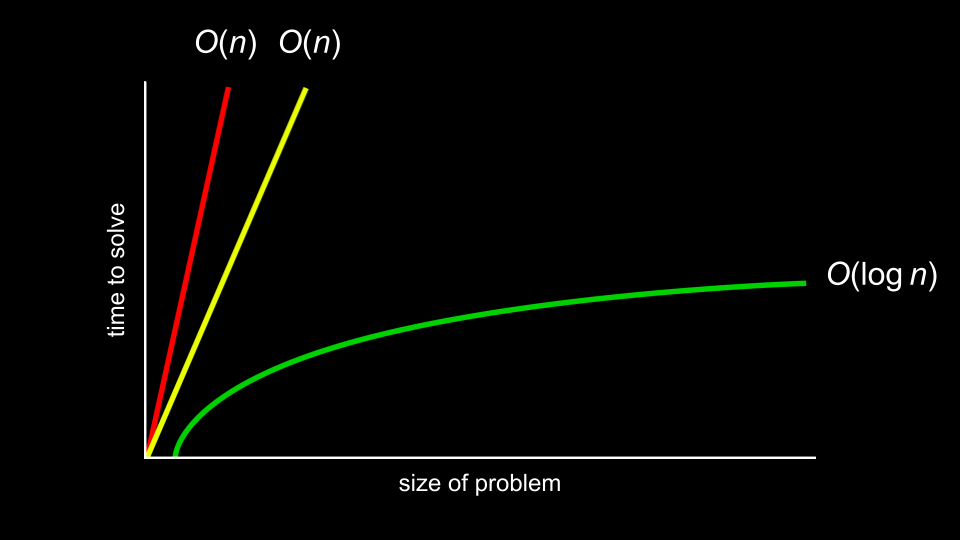
在图中,第一个算法的复杂度为 ,第二个算法的复杂度也为 ,第三个算法的复杂度为 。
曲线的形状反映了算法的效率。以下是一些常见的算法复杂度:
在这些复杂度中, 被认为是最差的, 是最好的。
线性搜索的复杂度为 ,因为在最坏情况下,它可能需要执行 n 步。
二分搜索的复杂度为 ,即使在最坏情况下,其执行步骤也会随着问题规模的增大而越来越少。
程序员通常关注算法的最坏情况(即上限)和最佳情况(即下限)。
符号表示算法的最佳情况复杂度,例如 。
符号表示算法的上限和下限相同,即最佳情况和最坏情况具有相同的复杂度。
线性搜索和二分搜索
你可以通过在终端窗口输入
code search.c命令,然后编写以下代码来实现线性搜索:#include <cs50.h>
#include <stdio.h>
int main(void)
{
// 一个整数数组
int numbers[] = {20, 500, 10, 5, 100, 1, 50};
// 搜索数字
int n = get_int("Number: ");
for (int i = 0; i < 7; i++)
{
if (numbers[i] == n)
{
printf("Found\n");
return 0;
}
}
printf("Not found\n");
return 1;
}注意,
int numbers[]这一行允许我们在创建数组的同时初始化每个元素的值。 之后,在for循环中,我们实现了线性搜索。我们现在已经在 C 语言中实现了线性搜索!
如果想在一个字符串数组中进行搜索,可以修改代码如下:
#include <cs50.h>
#include <stdio.h>
#include <string.h>
int main(void)
{
// 一个字符串数组
string strings[] = {"battleship", "boot", "cannon", "iron", "thimble", "top hat"};
// 搜索字符串
string s = get_string("String: ");
for (int i = 0; i < 6; i++)
{
if (strcmp(strings[i], s) == 0)
{
printf("Found\n");
return 0;
}
}
printf("Not found\n");
return 1;
}注意,这里不能直接使用
==来比较字符串,而需要使用string.h库中的strcmp函数。实际上,运行这段代码可以让我们遍历这个字符串数组,检查是否包含某个特定的字符串。但是,如果遇到段错误,表明程序访问了不该访问的内存区域,请检查代码,确保循环条件是
i < 6而不是i < 7。我们可以将数字和字符串的概念结合起来,编写一个程序。在您的终端窗口中键入
code phonebook.c并编写如下代码:#include <cs50.h>
#include <stdio.h>
#include <string.h>
int main(void)
{
// 字符串数组
string names[] = {"Carter", "David"};
string numbers[] = {"+1-617-495-1000", "+1-949-468-2750"};
// 搜索姓名
string name = get_string("Name: ");
for (int i = 0; i < 2; i++)
{
if (strcmp(names[i], name) == 0)
{
printf("Found %s\n", numbers[i]);
return 0;
}
}
printf("Not found\n");
return 1;
}注意,Carter的电话号码以
+1-617开头,David的电话号码以1-949开头。因此,names[0]对应Carter,numbers[0]对应Carter的电话号码。虽然这段代码能实现功能,但效率不高,且姓名和电话号码可能不匹配。如果能创建自定义数据类型,将姓名和电话号码关联起来,就更好了。
数据结构
实际上,C 语言允许我们使用
struct创建自定义数据类型。修改您的代码如下:#include <cs50.h>
#include <stdio.h>
#include <string.h>
typedef struct
{
string name;
string number;
}
person;
int main(void)
{
person people[2];
people[0].name = "Carter";
people[0].number = "+1-617-495-1000";
people[1].name = "David";
people[1].number = "+1-949-468-2750";
// 搜索姓名
string name = get_string("Name: ");
for (int i = 0; i < 2; i++)
{
if (strcmp(people[i].name, name) == 0)
{
printf("Found %s\n", people[i].number);
return 0;
}
}
printf("Not found\n");
return 1;
}注意,代码以
typedef struct开头,定义了一个名为person的新数据类型,包含name和number两个字符串成员。在main函数中,创建了一个person类型的数组people,大小为 2。我们随后更新了数组中两个人的姓名和电话号码。重点是,通过点表示法 (如people[0].name),我们可以访问数组中特定位置的person对象的成员。
排序
排序指的是将未排序的值列表转换为已排序列表的过程。
当列表被排序后,搜索该列表对计算机的负担要小得多。回想一下,我们可以在已排序的列表上使用二分查找,但不能在未排序的列表上使用。
事实证明,有许多不同类型的排序算法。
选择排序就是这样一种搜索算法。
选择排序的伪代码如下:
对于 i 从 0 到 n–1:
查找 numbers[i] 到 numbers[n-1] 之间的最小数字
将最小数字与 numbers[i] 交换考虑以下未排序的列表:
选择排序会首先找到列表中最小的数字,然后将其与当前位置的数字交换。 在这个例子中,找到了数字0,并将其移动到了当前位置。
现在,问题规模缩小了,因为我们至少知道列表的起始部分已经排好序。 因此,我们可以从列表的第二个数字开始,重复上述步骤。
现在,1是最小的数字,所以我们将其与第二个数字交换。 接下来,重复这个过程……
……以此类推……
……以此类推……
……以此类推……
……以此类推……
冒泡排序 是另一种排序算法,它通过不断交换相邻元素,使得较大的元素像气泡一样“冒”到末尾。
冒泡排序的伪代码是:
重复 n-1 次
对于 i 从 0 到 n–2
如果 numbers[i] 大于 numbers[i+1]
交换它们我们从这个未排序的列表开始。 这一次,我们将查看每对相邻的数字,如果前一个数字大于后一个数字,就交换它们:
5 2 7 4 1 6 3 0
^ ^
2 5 7 4 1 6 3 0
^ ^
2 5 7 4 1 6 3 0
^ ^
2 5 4 7 1 6 3 0
^ ^
2 5 4 1 7 6 3 0
^ ^
2 5 4 1 6 7 3 0
^ ^
2 5 4 1 6 3 7 0
^ ^
2 5 4 1 6 3 0 7现在,最大的数字已经被移动到了最右侧,所以问题得到了一定的解决。 接下来,我们再次重复这个过程:
2 5 4 1 6 3 0 | 7
^ ^
2 5 4 1 6 3 0 | 7
^ ^
2 4 5 1 6 3 0 | 7
^ ^
2 4 1 5 6 3 0 | 7
^ ^
2 4 1 5 6 3 0 | 7
^ ^
2 4 1 5 3 6 0 | 7
^ ^
2 4 1 5 3 0 6 | 7现在,两个最大的数字都位于右侧。 我们再次重复这个过程:
2 4 1 5 3 0 | 6 7
^ ^
2 4 1 5 3 0 | 6 7
^ ^
2 1 4 5 3 0 | 6 7
^ ^
2 1 4 5 3 0 | 6 7
^ ^
2 1 4 3 5 0 | 6 7
^ ^
2 1 4 3 0 5 | 6 7……以此类推……
2 1 4 3 0 | 5 6 7
^ ^
1 2 4 3 0 | 5 6 7
^ ^
1 2 3 4 0 | 5 6 7
^ ^
1 2 3 4 0 | 5 6 7
^ ^
1 2 3 0 4 | 5 6 7……以此类推……
1 2 3 0 | 4 5 6 7
^ ^
1 2 3 0 | 4 5 6 7
^ ^
1 2 3 0 | 4 5 6 7
^ ^
1 2 0 3 | 4 5 6 7… 再次…
1 2 0 | 3 4 5 6 7
^ ^
1 2 0 | 3 4 5 6 7
^ ^
1 0 2 | 3 4 5 6 7… 最终 …
1 0 | 2 3 4 5 6 7
^ ^
0 1 | 2 3 4 5 6 7注意,随着列表遍历的进行,越来越多的部分变得有序,因此我们只需要关注尚未排序的数字对。
用数学方式表示,其中 n 代表元素的数量,那么选择排序的分析过程可以表示为:
(n-1)+(n-2)+(n-3)+ ... + 1或者,更简单地说 \(n^2/2 - n/2\)。
根据上述数学分析,n² 是决定算法效率的最关键因素。因此,在所有元素都未排序的最坏情况下,选择排序的时间复杂度被认为是 \(O(n^2)\)。即使所有元素都已经排序,算法仍然需要执行相同的步骤。因此,最佳情况也可以表示为 \(\Omega(n^2)\)。由于其最坏情况和最佳情况的时间复杂度相同,因此选择排序的平均时间复杂度可以被认为是 \(\Theta(n^2)\)。
分析冒泡排序,最坏情况是 \(O(n^2)\)。最佳情况是 \(\Omega(n)\)。
您可以可视化 这些算法的比较。
递归
我们该如何提高排序的效率呢?
递归 是编程中的一个概念,其中函数调用自身。我们之前看到过这种情况,当我们看到…
If no doors
Return false
If number behind middle door
Return true
Else if number < middle door
Search left half
Else if number > middle door
Search right half请注意,我们正在对这个问题的越来越小的迭代调用
search。同样,在第零周的伪代码中,您可以看到递归的实现位置:
1 拿起电话簿
2 翻到电话簿的中间
3 看页面
4 如果此人在页面上
5 给这个人打电话
6 否则,如果此人在书中较早
7 翻到书的左半部分的中间
8 回到第 3 行
9 否则,如果此人在书中较晚
10 翻到书的右半部分的中间
11 回到第 3 行
12 Else
13 退出回顾一下在第一周,我们希望创建一个如下所示的金字塔结构:
要使用递归实现此目的,请在终端窗口中键入
code recursion.c并编写如下代码:#include <cs50.h>
#include <stdio.h>
void draw(int n);
int main(void)
{
draw(1);
}
void draw(int n)
{
for (int i = 0; i < n; i++)
{
printf("#");
}
printf("\n");
draw(n + 1);
}请注意,
draw函数会调用自身。此外,请注意您的代码可能进入无限循环。如果程序陷入死循环,可以按Ctrl+C来终止程序。产生无限循环的原因是没有设置程序终止的条件,缺少基本情况(base case)。我们可以如下更正我们的代码:
#include <cs50.h>
#include <stdio.h>
void draw(int n);
int main(void)
{
// Get height of pyramid
int height = get_int("Height: ");
// Draw pyramid
draw(height);
}
void draw(int n)
{
// If nothing to draw
if (n <= 0)
{
return;
}
// Draw pyramid of height n - 1
draw(n - 1);
// Draw one more row of width n
for (int i = 0; i < n; i++)
{
printf("#");
}
printf("\n");
}请注意,基本情况(base case) 将确保代码不会永远运行。
if (n <= 0)行终止了递归,因为问题已得到解决。 每次draw函数递归调用自身时,传入的参数是n-1。 当n-1最终等于0时,draw函数将返回,从而结束递归调用。
归并排序 (Merge Sort)
现在,我们可以利用递归来实现一种更高效的排序算法,即归并排序 (Merge Sort),这是一种非常高效的排序算法。
归并排序 (Merge Sort) 的伪代码非常简短:
如果只有一个数字
退出
否则
对左半部分数字进行排序
对右半部分数字进行排序
合并排序后的两半考虑以下数字列表:
归并排序 (Merge Sort) 首先判断:“当前序列是否只包含一个数字?” 如果答案为“否”,算法将继续执行。
其次,归并排序 (Merge Sort) 现在会将数字从中间(或尽可能接近)分割开,并对左半部分数字进行排序。
第三,归并排序 (Merge Sort) 会查看左侧的这些数字并询问:“这是一个数字吗?” 由于答案是否定的,它会将左侧的数字从中间分割开。
第四,归并排序 (Merge Sort) 将再次询问,“这是一个数字吗?” 这次答案是肯定的! 因此,它将退出此任务并返回到此时正在运行的最后一个任务:
第五,归并排序 (Merge Sort) 将对左侧的数字进行排序。
现在,我们回到伪代码中上次停止的地方,现在左侧已经排序。 对右半部分数字执行类似步骤3-5的过程。 结果是:
现在两半都已排序。 最后,该算法将合并两侧。 它将查看左侧的第一个数字和右侧的第一个数字。 它将把较小的数字放在第一位,然后是第二小的数字。 算法对所有数字重复执行此操作,最终得到:
归并排序 (Merge Sort) 完成,程序退出。
归并排序 (Merge Sort) 是一种非常高效的排序算法,最坏情况为 \(O(n \log n)\)。 最佳情况仍然是 \(\Omega(n \log n)\),因为该算法仍然必须访问列表中的每个位置。 因此,归并排序 (Merge Sort) 也是 \(\Theta(n \log n)\),因为最佳情况和最坏情况相同。
最后,分享了一个[可视化]链接。
总结
在本课程中,您学习了算法思维和构建自定义数据类型的方法。 具体来说,您学习了……
- 算法 (Algorithms)。
- 大O表示法 (Big O notation)。
- 二分查找与线性查找 (Binary search and linear search)。
- 各种排序算法,例如冒泡排序、选择排序和归并排序。
- 递归。
下次见!