第五讲 - CS50x 2023
欢迎!
- 之前的几周我们已经介绍了编程的基本构建块。
- 你所学的 C 语言知识将帮助你在 Python 等更高级的编程语言中实现这些基本模块。
- 今天,我们将讨论如何在内存中组织数据。
数据结构
- 数据结构 本质上是内存中的组织形式。
- 有很多方法可以在内存中组织数据。
- 抽象数据结构 是指我们可以在概念层面进行想象的数据结构。 在学习计算机科学时,通常从这些概念性的数据结构入手会很有帮助。 学习这些概念将使你更容易理解如何实现更具体的数据结构。
栈和队列
队列 是一种抽象数据结构之一。
队列具有特定的属性。 也就是说,它们是 FIFO,或“先进先出”。 你可以想象一下在游乐园排队等候游乐设施的场景。 排在队伍最前面的人先乘坐,最后面的人最后乘坐。
队列具有与其相关的特定操作。 例如,一个项目可以被 入队,即加入队列。 此外,一个项目可以被 出队,也就是从队伍最前面离开队列。
队列和栈是相对的。 本质上,栈的属性与队列不同。 具体来说,它是 LIFO,或“后进先出”。 就像在自助餐厅堆叠托盘,最后放上去的托盘总是最先被取走的。
栈具有与其相关的特定操作。 例如,push 操作将元素放置在栈顶,而 pop 操作则从栈顶移除元素。
在代码中,你可以想象一个栈如下所示:
const int CAPACITY = 50;
typedef struct
{
person people[CAPACITY];
int size;
}
stack;注意,名为
people的数组,其元素类型为person。CAPACITY定义了栈的最大容量。 整数size表示栈当前存储的元素数量,即使栈的容量更大。你可能已经注意到上面的代码存在一个局限性。 因为数组的容量是在代码中预先定义的。 因此,栈可能会占用过多的内存空间。 你可能会遇到栈只使用了一个位置,但却预留了 5000 个位置的情况。
如果我们的栈能够动态调整大小,随着元素的添加自动增长,那就更好了。
Jack 学习事实
- 我们观看了一段由埃隆大学 Shannon Duvall 教授制作的视频,名为 Jack Learns the Facts。
调整数组尺寸
回顾第二周的内容,我们介绍了你接触的第一个数据结构。
数组是一段连续的内存块。
你可以将数组想象成如下形式:
在内存中,还存储着其他程序、函数和变量的数据。 其中很多可能是之前使用过但现在已经废弃的垃圾数据。

假设你想在数组中存储第四个值
4,该怎么办? 这时,我们需要分配一块新的内存区域,并将旧数组的数据复制到新的区域。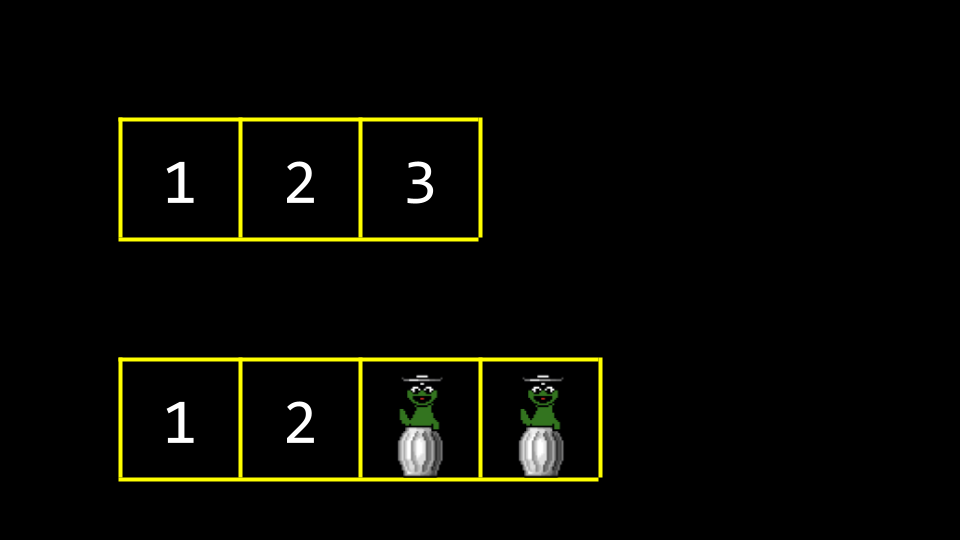
旧的垃圾数据会被新数据覆盖。
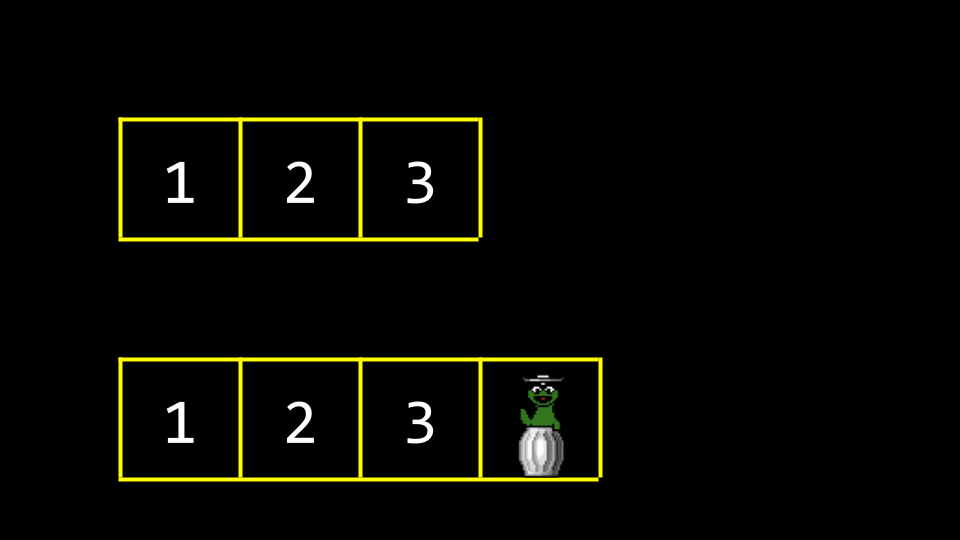
这种方法的一个缺点是效率低:每次添加数字,都需要逐个复制数组元素。
如果能把
4放在内存中的其他地方,岂不是更好? 但这样一来,根据数组的定义,4就不再和之前的元素连续存储,也就不再是数组了。在您的终端中,键入
code list.c并编写如下代码:// 使用固定大小的数组实现数字列表
#include <stdio.h>
int main(void)
{
// 大小为 3 的列表
int list[3];
// 使用数字初始化列表
list[0] = 1;
list[1] = 2;
list[2] = 3;
// 打印列表
for (int i = 0; i < 3; i++)
{
printf("%i\n", list[i]);
}
}请注意,以上代码和我们之前学过的很相似,都是预先分配了三个元素的内存空间。
基于我们最近学到的知识,可以利用指针来优化代码设计。 请按照如下方式修改代码:
// 使用动态大小的数组实现数字列表
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
// 大小为 3 的列表
int *list = malloc(3 * sizeof(int));
if (list == NULL)
{
return 1;
}
// 使用数字初始化大小为 3 的列表
list[0] = 1;
list[1] = 2;
list[2] = 3;
// 大小为 4 的列表
int *tmp = malloc(4 * sizeof(int));
if (tmp == NULL)
{
free(list);
return 1;
}
// 将大小为 3 的列表复制到大小为 4 的列表
for (int i = 0; i < 3; i++)
{
tmp[i] = list[i];
}
// 将数字添加到大小为 4 的列表
tmp[3] = 4;
// 释放大小为 3 的列表
free(list);
// 记住大小为 4 的列表
list = tmp;
// 打印列表
for (int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
// 释放列表
free(list);
return 0;请注意,代码首先创建了一个可以容纳3个整数的列表。 接着,将内存地址中的值依次赋值为
1、2和3。 然后,创建一个可以容纳4个整数的列表。 接下来,将原列表的内容复制到新列表中,并将值4添加到新列表tmp的末尾。 由于list原先指向的内存块不再使用,因此使用free(list)命令释放该内存。 最后,将list指针指向tmp所指向的新的内存块。 打印list的内容,并释放内存。可以将
list和tmp看作是指向内存块的标签。 如上例所示,list最初指向一个大小为3的数组。 最后,list指向一个大小为4的内存块。 实际上,在代码执行完毕后,tmp和list指向的是同一块内存。C语言提供了一个非常有用的函数
realloc,它能帮你重新分配内存。realloc接受两个参数。首先,它会让你指定想要复制的数组。其次,它会让你指定最终数组的期望大小。请按照如下方式修改你的代码:// 使用 realloc 实现动态大小的数字列表
#include <stdio.h>
#include <stdlib.h>
int main(void)
{
// 大小为 3 的列表
int *list = malloc(3 * sizeof(int));
if (list == NULL)
{
return 1;
}
// 使用数字初始化大小为 3 的列表
list[0] = 1;
list[1] = 2;
list[2] = 3;
// 将列表大小调整为 4
int *tmp = realloc(list, 4 * sizeof(int));
if (tmp == NULL)
{
free(list);
return 1;
}
list = tmp;
// 向列表添加数字
list[3] = 4;
// 打印列表
for (int i = 0; i < 4; i++)
{
printf("%i\n", list[i]);
}
// 释放列表
free(list);
return 0;
}请注意,
int *tmp = realloc(list, 4 * sizeof(int))尝试将列表的大小调整为 4 个整数的大小。然后,它会将list中的值复制到这个新数组中。最后,指针tmp指向这个新数组的内存地址。realloc函数负责处理复制操作。如果realloc分配了新的内存块,那么list原先指向的内存会被释放。然后,指针list指向tmp指向的内存地址,也就是新数组的地址。可以想象一下,将
realloc应用于队列或堆栈会非常有用。随着数据量的增长,可以使用realloc来增大或缩小堆栈或队列。
链表
最近几周,你学习了三个很有用的基本概念。
struct是一种可以自定义的数据类型。.(点运算符) 允许你访问结构体内部的变量。*运算符用于声明指针或者解引用。今天,我们将介绍
->运算符。这个运算符可以访问指针指向的结构体内部成员。链表是 C 语言中最强大的数据结构之一。链表允许你存储位于不同内存地址的数据。此外,链表还能根据需要动态地扩展或缩小。
可以想象有三个值存储在不同的内存区域,如下图所示:
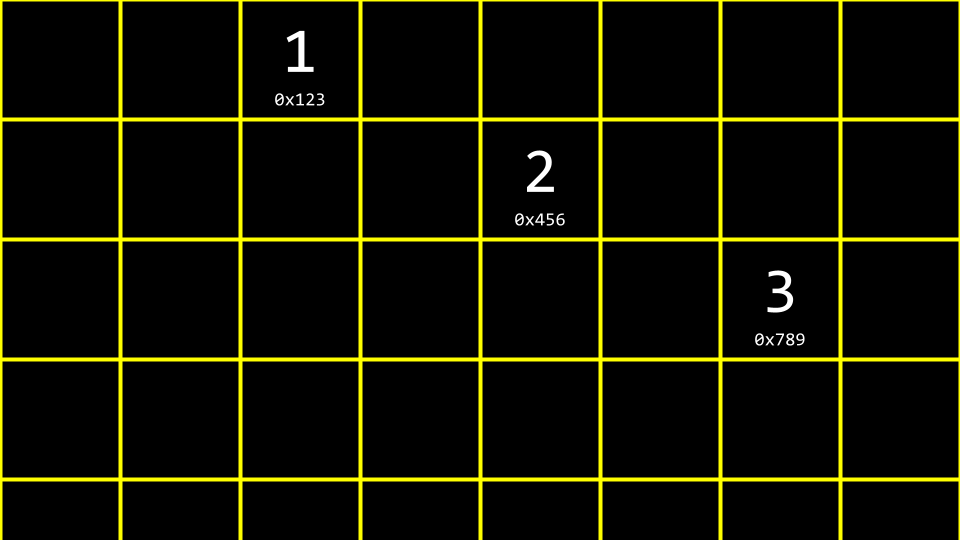
如何将这些值串联成一个列表呢?
我们可以想象上面这张图中的数据如下所示:
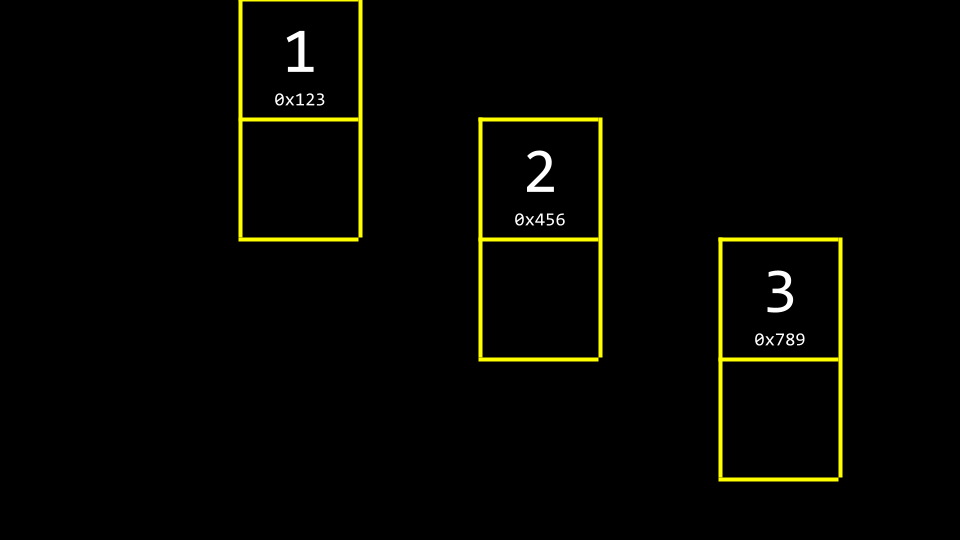
我们需要额外的内存来记录下一个元素的位置。
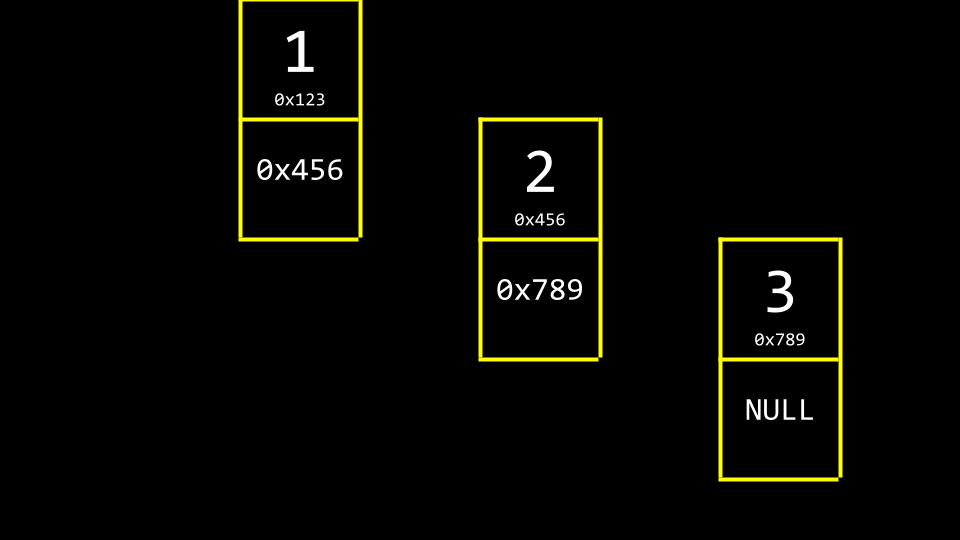
注意,
NULL用于表示这是列表的末尾,没有下一个元素了。按照惯例,我们会在内存中保留一个额外的元素,一个指针,用于跟踪列表中的第一个项目。
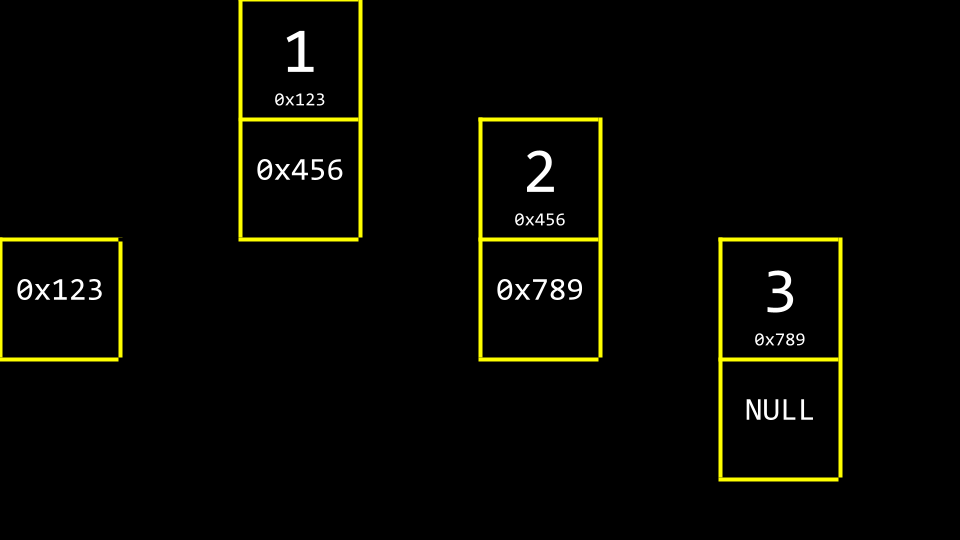
抽象掉内存地址,列表将如下所示:
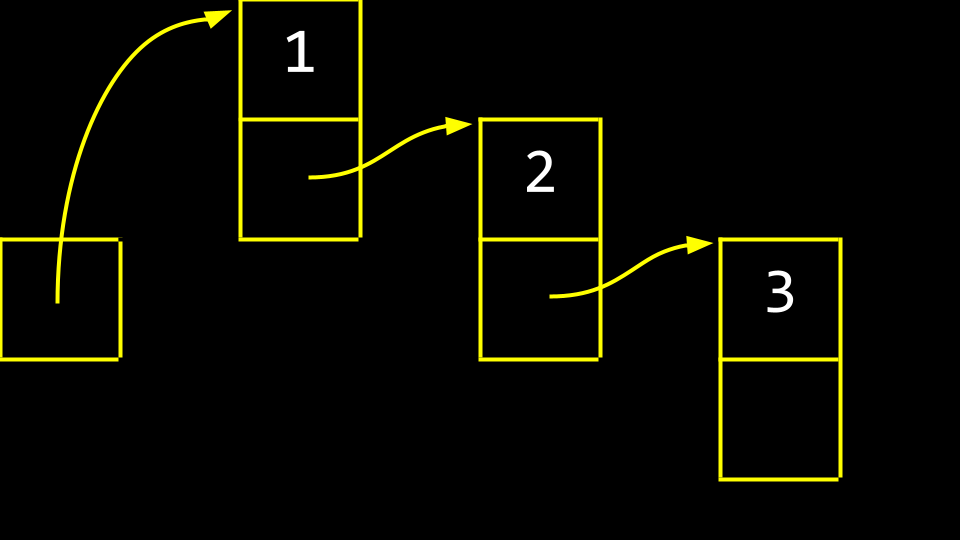
这些方框被称为节点 (nodes)。一个节点包含一个数据项 (item) 和一个名为 next 的指针。在代码中,你可以这样想象一个节点:
typedef struct node
{
int number;
struct node *next;
}
node;请注意,此节点中包含的数据是一个名为
number的整数。其次,包含一个名为next的指针,它指向内存中的另一个节点。链表不存储在连续的内存块中。只要有足够的系统资源,它们就可以按需增长。然而,与数组相比,链表需要更多的内存来维护其结构,这是它的一个缺点。这是因为除了元素本身的值,还需要额外存储指向下一个节点的指针。此外,链表不像数组那样支持随机访问(索引),因为要访问第 \(n\) 个元素,需要从头开始遍历前 \(n - 1\) 个元素。因此,上述链表只能进行线性搜索。因此,对于以上述方式构建的链表,无法使用二分查找。
从概念上讲,我们可以这样理解链表的创建过程。首先,声明
node *list,此时它的值是未定义的。
接下来,在内存中分配一个节点,并将其命名为
n。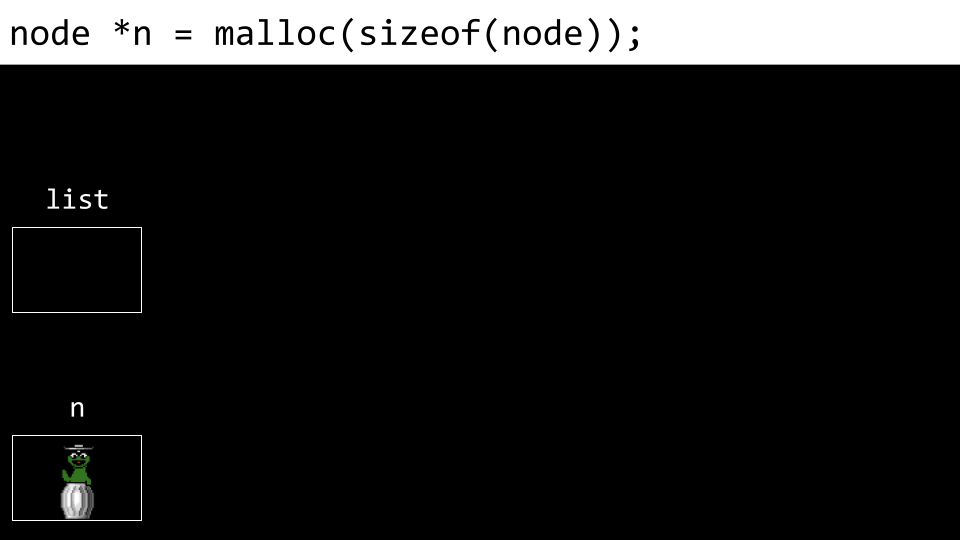
接下来,将节点
n的number字段赋值为1。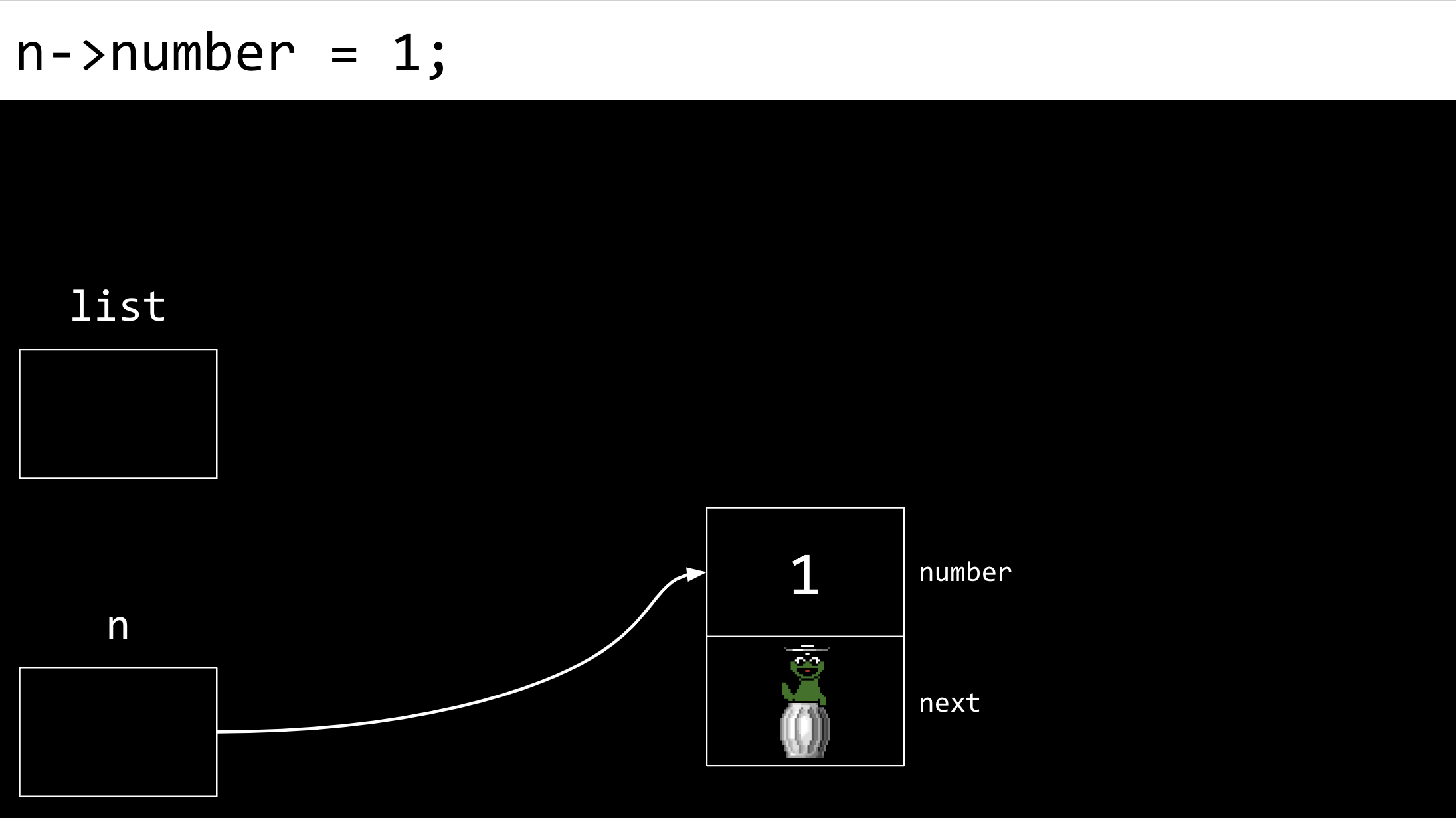
接下来,将节点
n的next字段赋值为NULL。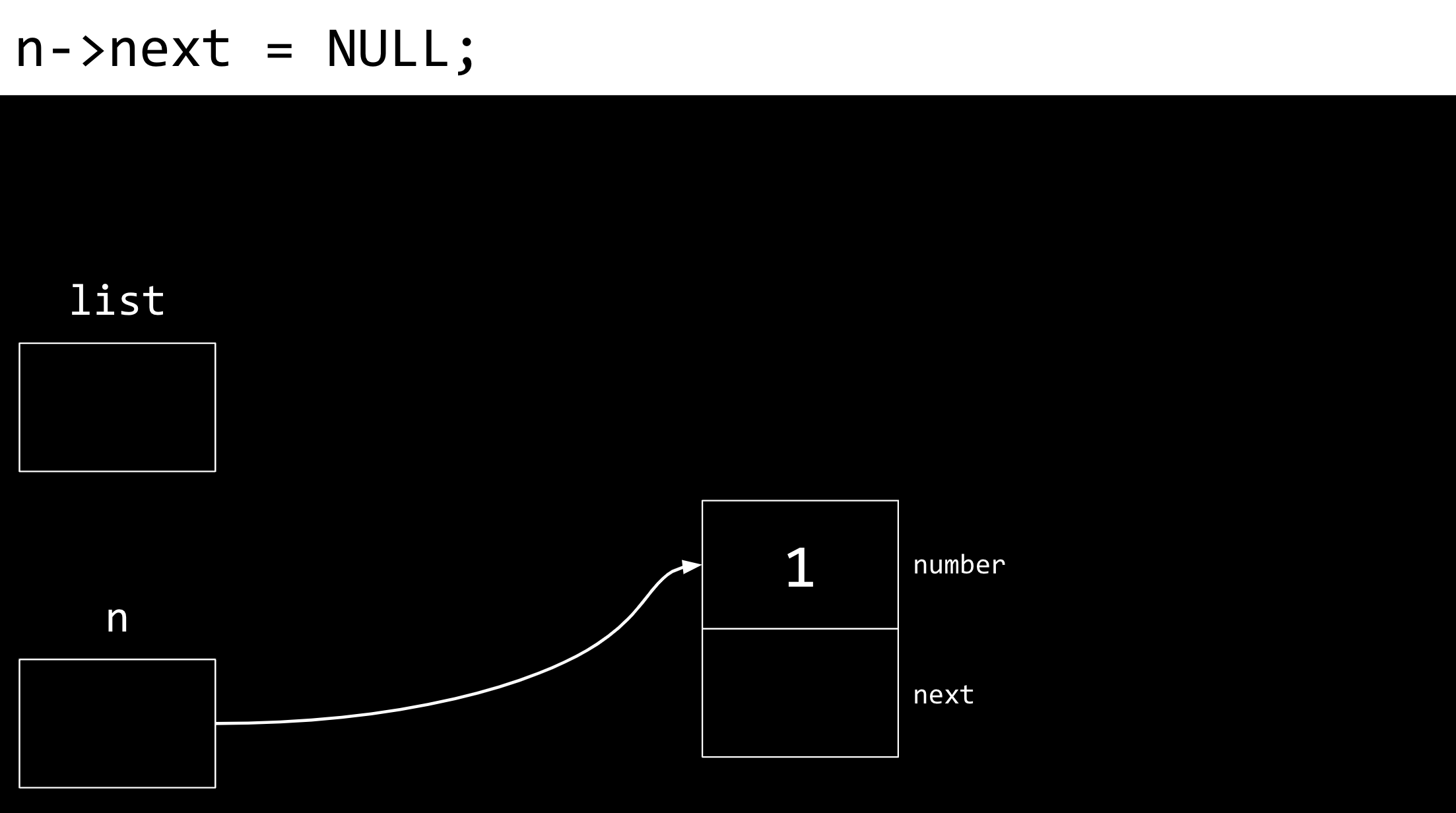
接下来,
list指向n指向的内存位置。n和list现在指向同一块内存地址。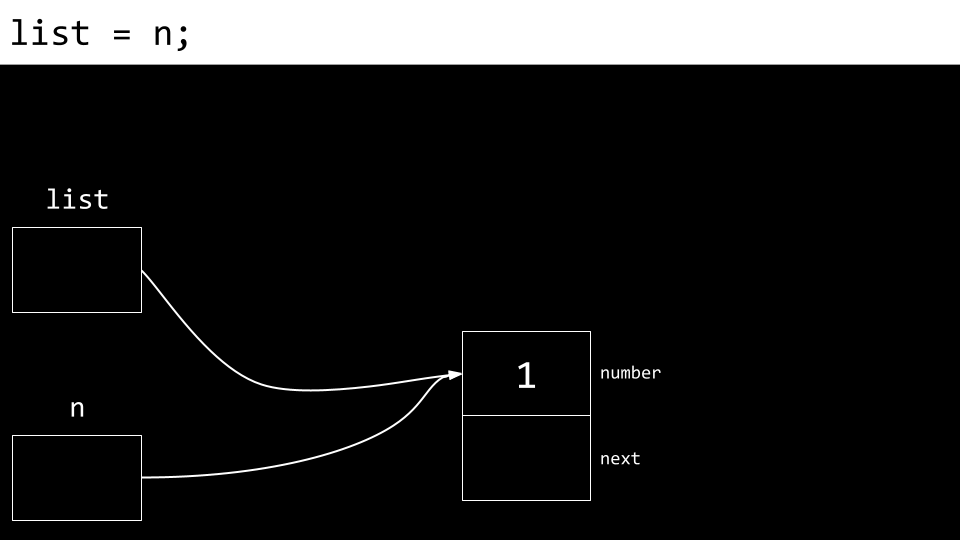
然后创建一个新节点。此时,
number和next字段的值都是未定义的。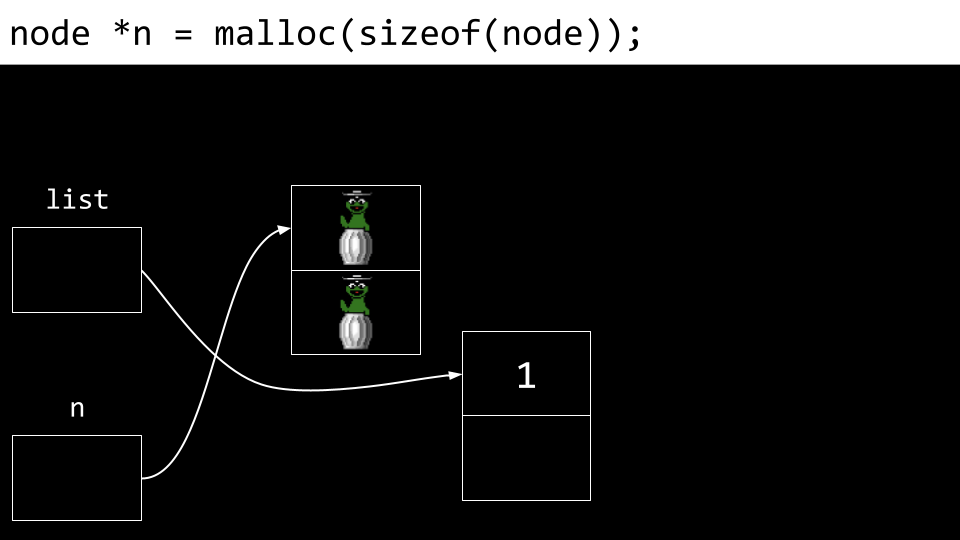
将新节点(
n)的number字段更新为2。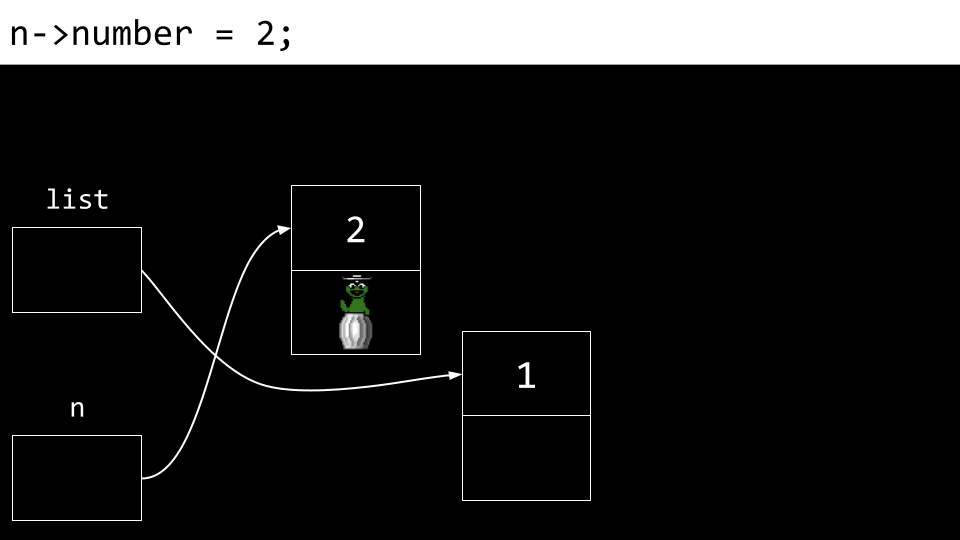
同样,也需要更新
next字段。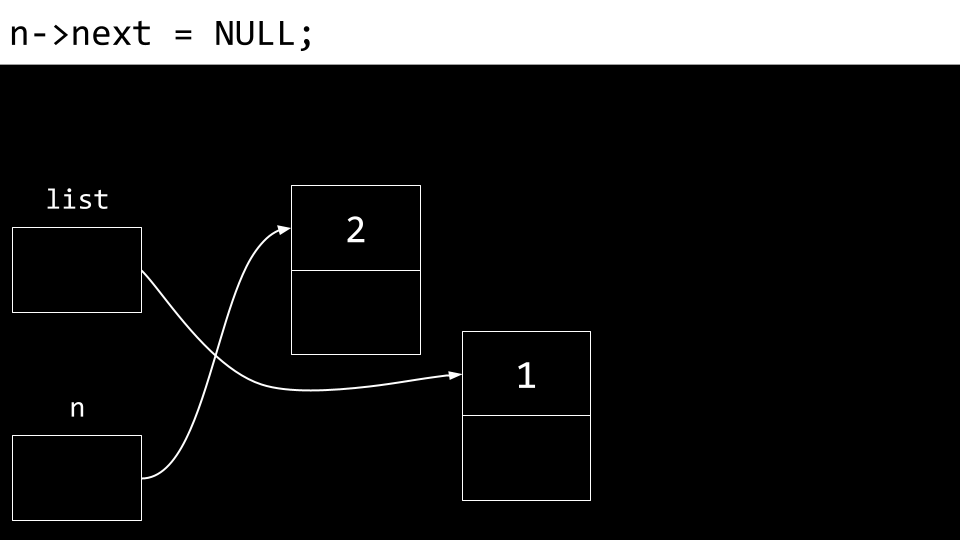
最重要的是,我们不能丢失对任何节点的引用,否则它们将无法访问。因此,将
n的next字段指向list当前指向的内存位置。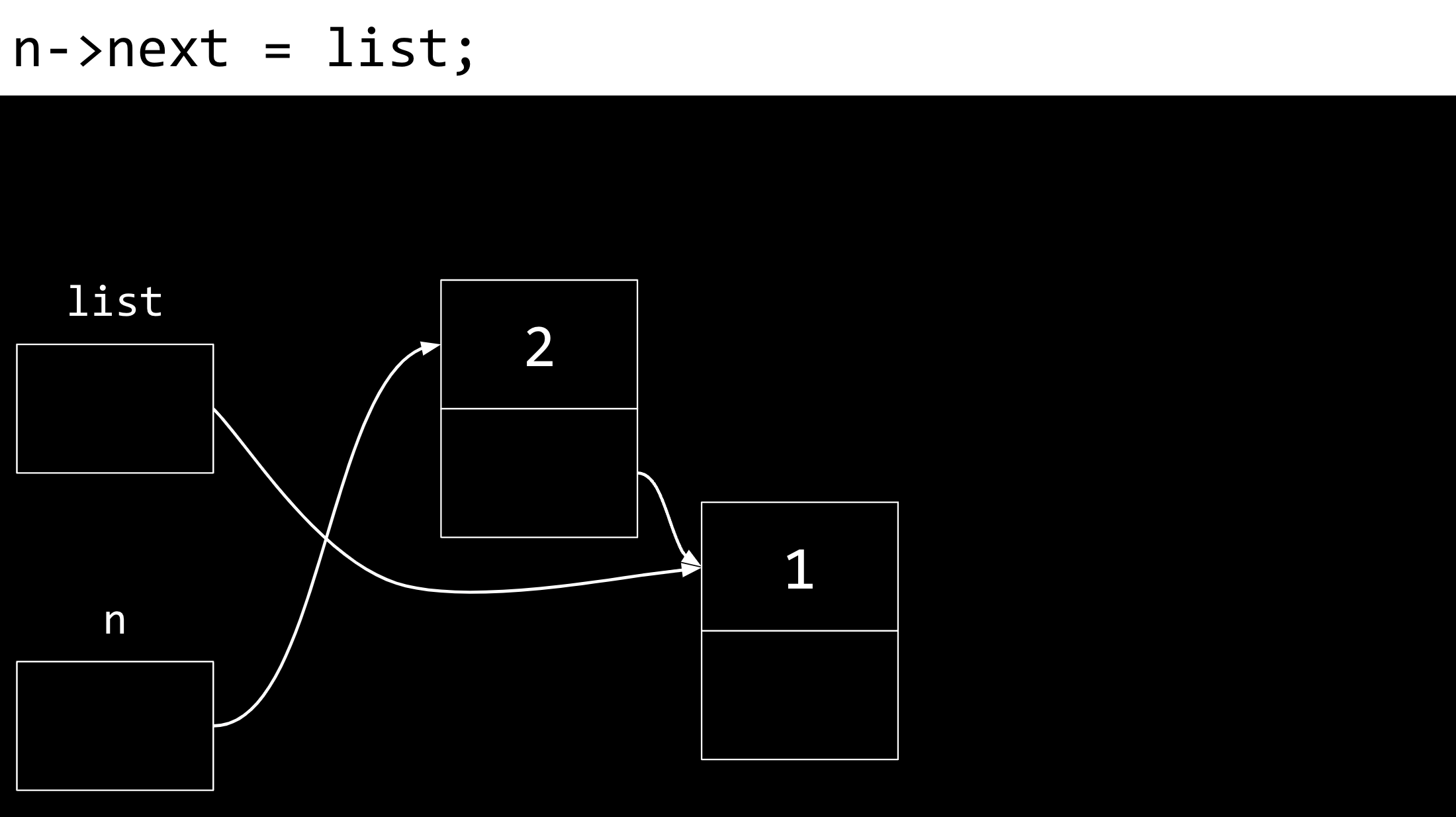
最后,更新
list使其指向n。我们现在有一个包含两个项目的链表。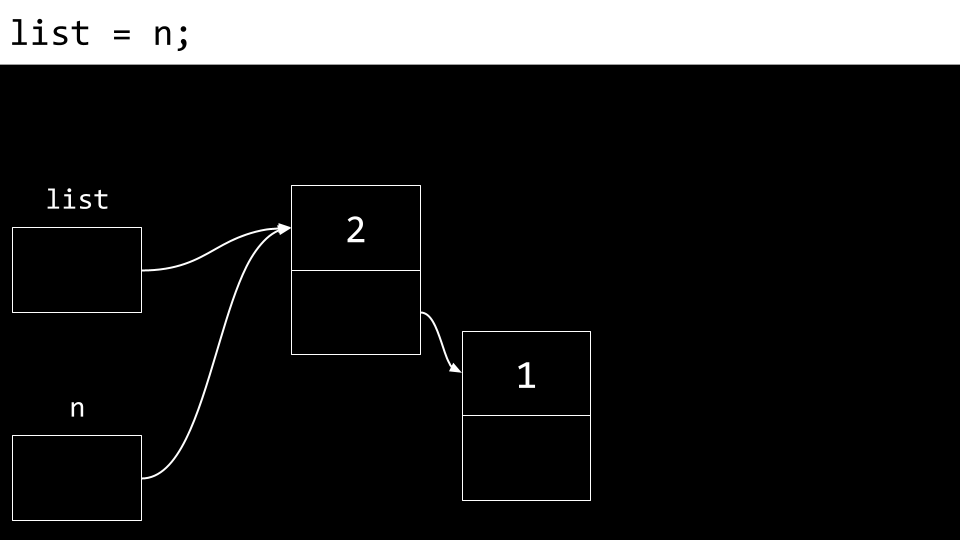
为了在代码中实现上述逻辑,请按如下方式修改你的代码:
// 使用while循环将数字前置到链表
#include <cs50.h>
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int number;
struct node *next;
}
node;
int main(int argc, char *argv[])
{
// 存储数字的内存
node *list = NULL;
// 对于每个命令行参数
for (int i = 1; i < argc; i++)
{
// 把参数转换成整数
int number = atoi(argv[i]);
// 为数字分配一个节点
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = number;
n->next = NULL;
// 将节点添加到链表头部
n->next = list;
list = n;
}
// 打印数字
node *ptr = list;
while (ptr != NULL)
{
printf("%i\n", ptr->number);
ptr = ptr->next;
}
// 释放内存
ptr = list;
while (ptr != NULL)
{
node *next = ptr->next;
free(ptr);
ptr = next;
}
}请注意,用户在命令行输入的数字会被存入名为
n的节点的number字段,然后该节点会被添加到链表中。例如,./list 1 2会将数字1放入名为n的节点的number字段中,然后将指向list的指针存入该节点的next字段,并将list更新为指向n。对于数字2,重复上述过程。接下来,node *ptr = list创建了一个临时变量ptr,它指向list所指向的地址。while循环打印ptr所指向节点的内容,然后将ptr更新为指向链表中的下一个节点。最后,所有内存都会被释放。其时间复杂度为\(O(n)\),因为在最坏情况下,必须搜索整个链表才能找到目标元素。向链表添加新元素的时间复杂度取决于添加位置。以下示例说明了这一点。
例如,以下代码实现了一个将数字前置到链表的程序:
// 使用 for 循环将数字前置到链表
#include <cs50.h>
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int number;
struct node *next;
}
node;
int main(int argc, char *argv[])
{
// 存储数字的内存
node *list = NULL;
// 对于每个命令行参数
for (int i = 1; i < argc; i++)
{
// 把参数转换成整数
int number = atoi(argv[i]);
// 为数字分配一个节点
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = number;
n->next = NULL;
// 将节点添加到链表头部
n->next = list;
list = n;
}
// 打印数字
for (node *ptr = list; ptr != NULL; ptr = ptr->next)
{
printf("%i\n", ptr->number);
}
// 释放内存
node *ptr = list;
while (ptr != NULL)
{
node *next = ptr->next;
free(ptr);
ptr = next;
}
}请注意,数字是如何放置在列表的开头的。这种前置操作的时间复杂度为\(O(1)\),因为所需步骤与链表大小无关。
此外,您也可以将数字添加到链表的末尾,如下面的代码所示:
// 使用链表实现数字列表
#include <cs50.h>
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int number;
struct node *next;
}
node;
int main(int argc, char *argv[])
{
// Memory for numbers
node *list = NULL;
// For each command-line argument
for (int i = 1; i < argc; i++)
{
// Convert argument to int
int number = atoi(argv[i]);
// Allocate node for number
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = number;
n->next = NULL;
// If list is empty
if (list == NULL)
{
// This node is the whole list
list = n;
}
// If list has numbers already
else
{
// Iterate over nodes in list
for (node *ptr = list; ptr != NULL; ptr = ptr->next)
{
// If at end of list
if (ptr->next == NULL)
{
// Append node
ptr->next = n;
break;
}
}
}
}
// Print numbers
for (node *ptr = list; ptr != NULL; ptr = ptr->next)
{
printf("%i\n", ptr->number);
}
// Free memory
node *ptr = list;
while (ptr != NULL)
{
node *next = ptr->next;
free(ptr);
ptr = next;
}
}注意这段代码是如何“遍历”链表来找到尾部的。当在链表尾部添加一个元素时,我们的代码的时间复杂度是 \(O(n)\),因为我们需要遍历整个链表才能找到尾部并添加新元素。
此外,你也可以在添加元素的同时对链表进行排序:
// Implements a sorted list of numbers using a linked list
#include <cs50.h>
#include <stdio.h>
#include <stdlib.h>
typedef struct node
{
int number;
struct node *next;
}
node;
int main(int argc, char *argv[])
{
// Memory for numbers
node *list = NULL;
// For each command-line argument
for (int i = 1; i < argc; i++)
{
// Convert argument to int
int number = atoi(argv[i]);
// Allocate node for number
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = number;
n->next = NULL;
// If list is empty
if (list == NULL)
{
list = n;
}
// If number belongs at beginning of list
else if (n->number < list->number)
{
n->next = list;
list = n;
}
// If number belongs later in list
else
{
// Iterate over nodes in list
for (node *ptr = list; ptr != NULL; ptr = ptr->next)
{
// If at end of list
if (ptr->next == NULL)
{
// Append node
ptr->next = n;
break;
}
// If in middle of list
if (n->number < ptr->next->number)
{
n->next = ptr->next;
ptr->next = n;
break;
}
}
}
}
// Print numbers
for (node *ptr = list; ptr != NULL; ptr = ptr->next)
{
printf("%i\n", ptr->number);
}
// Free memory
node *ptr = list;
while (ptr != NULL)
{
node *next = ptr->next;
free(ptr);
ptr = next;
}
}注意,这个链表在构建的过程中就已经完成了排序。要按照这种方式插入元素,在最坏的情况下,我们需要遍历当前链表中的所有元素来找到合适的位置,因此每次插入的时间复杂度仍然是 \(O(n)\)。
Trees
二叉搜索树 是另一种数据结构,可用于更有效地存储数据,以便可以搜索和检索数据。
你可以想象一个已经排序好的数字序列。

现在,假设中心值成为树的根节点。小于该值的放在左侧,大于该值的放在右侧。
然后,可以使用指针指向每个内存区域的正确位置,从而连接这些节点。
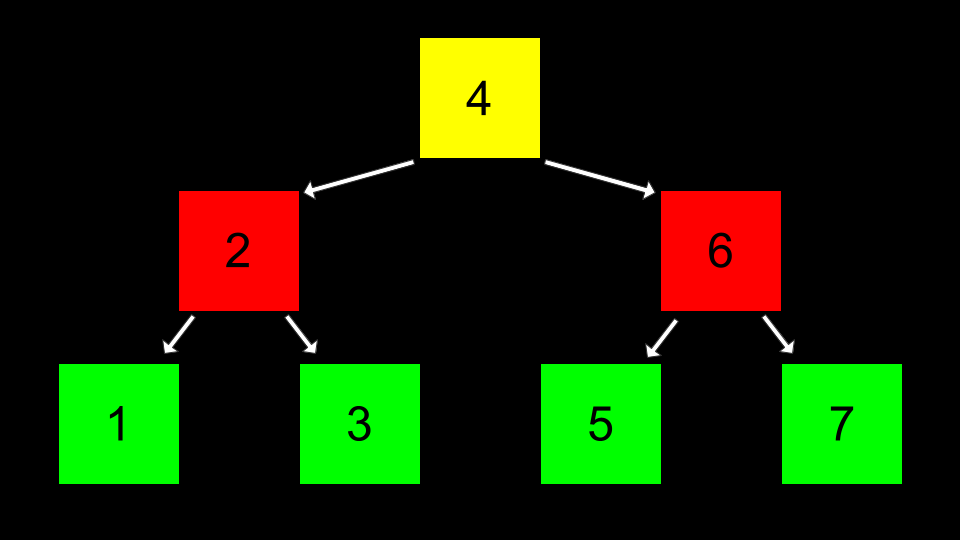
在代码中,这可以如下实现。
// 将数字列表实现为二叉搜索树
#include <stdio.h>
#include <stdlib.h>
// 表示一个节点
typedef struct node
{
int number;
struct node *left;
struct node *right;
}
node;
void free_tree(node *root);
void print_tree(node *root);
int main(void)
{
// 空树
node *tree = NULL;
// 添加数字到树中
node *n = malloc(sizeof(node));
if (n == NULL)
{
return 1;
}
n->number = 2;
n->left = NULL;
n->right = NULL;
tree = n;
// 加入数字
n = malloc(sizeof(node));
if (n == NULL)
{
free_tree(tree);
return 1;
}
n->number = 1;
n->left = NULL;
n->right = NULL;
tree->left = n;
// 插入数字
n = malloc(sizeof(node));
if (n == NULL)
{
free_tree(tree);
return 1;
}
n->number = 3;
n->left = NULL;
n->right = NULL;
tree->right = n;
// 打印树
print_tree(tree);
// 释放树
free_tree(tree);
return 0;
}
void free_tree(node *root)
{
if (root == NULL)
{
return;
}
free_tree(root->left);
free_tree(root->right);
free(root);
}
void print_tree(node *root)
{
if (root == NULL)
{
return;
}
print_tree(root->left);
printf("%i\n", root->number);
print_tree(root->right);
}以下是如何实现树的搜索:
bool search(node *tree, int number)
{
if (tree == NULL)
{
return false;
}
else if (number < tree->number)
{
return search(tree->left, number);
}
else if (number > tree->number)
{
return search(tree->right, number);
}
else if (number == tree->number)
{
return true;
}
}注意,此搜索函数首先访问
tree节点。然后,它使用递归来搜索number。与数组相比,上述树结构提供了更好的动态性,可以根据需要进行扩展或收缩。
字典
字典 是另一种数据结构。
像实际的书本形式的字典一样,字典有一个 键 和一个 值。
时间复杂度中最理想的情况是 \(O(1)\),即 常数时间。
这意味着访问速度几乎是瞬时的。
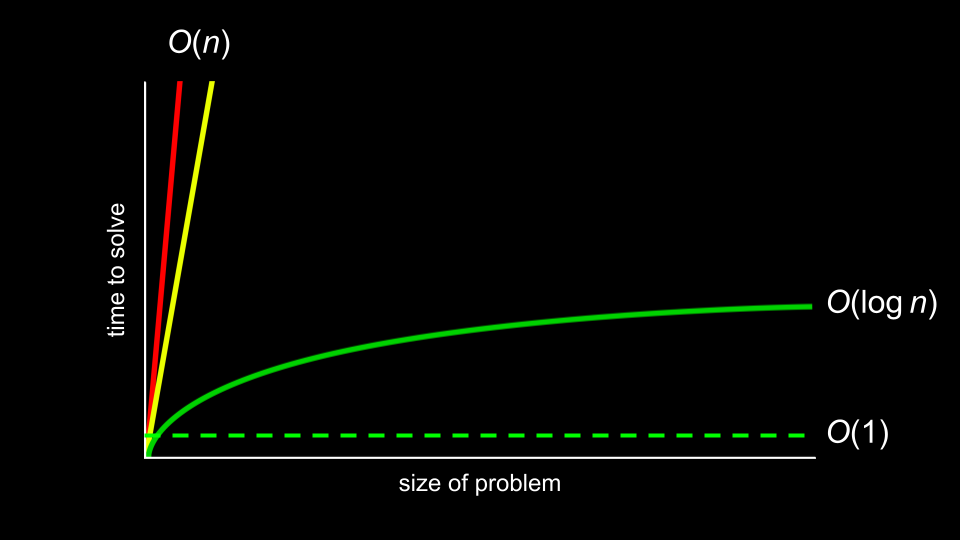
字典可以提供这种访问速度。
散列和散列表
散列是一种将一个值转换成另一个值,后者可以作为前者的快捷访问方式的概念。
例如,apple 经过散列函数计算后可能得到值
1,而 berry 可能得到2。因此,查找 apple 就像通过 散列 算法直接找到其存储位置一样简单。即使像将所有以 'a' 开头的词放在一个桶里,所有以 'b' 开头的词放在另一个桶里这种设计并不理想,但这种 分桶 的概念展示了如何利用散列值来快速定位数据。散列函数是一种将较大的输入值转换为较小且可预测的输出值的算法。
通常,该函数接收你想要添加到散列表中的数据项,并返回一个整数,该整数代表了该数据项应该被放置的数组索引。
散列表是数组和链表的巧妙结合。
从代码实现的角度来看,散列表可以看作是一个由指向 节点 (node) 的 指针 构成的 数组。
哈希表可以想象成如下:
请注意,这是一个数组,每个元素对应字母表中的一个字母。
接着,数组的每个位置都使用链表来存储对应的数据:

冲突指的是当尝试将一个值添加到散列表时,目标位置已经被占用。
在这种情况下,冲突的值会被简单地添加到链表的末尾。
通过优化散列表的设计和散列算法,可以减少冲突的发生。
一种改进的方案如下所示:

作为程序员,你需要权衡:是使用更多的内存来创建一个更大的散列表,从而潜在地减少搜索时间;还是使用更少的内存,但可能导致更长的搜索时间。
前缀树 (Trie)
前缀树是另一种数据结构。
前缀树的搜索时间复杂度始终为常数级别。
前缀树的一个缺点是它通常会占用大量的内存空间。
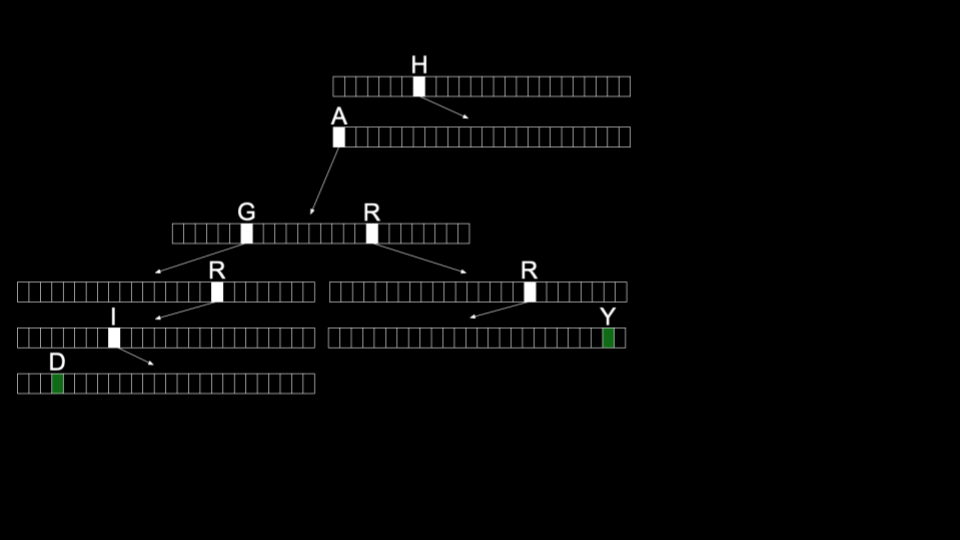
注意,仅仅为了存储 Hagrid 这个词,我们就需要 \(26 \times 5 = 130\) 个
节点 (node)!存储 Hagrid 的方式如下:

Harry 的存储方式类似,与 Hagrid 共享前两个字母 H 和 A。
总结一下
在本节课中,我们学习了如何利用指针构建新的数据结构,主要涉及以下内容……
- 数据结构
- 栈和队列
- 调整数组大小
- 链表
- 字典
- Tries
下次见!