Skip to main content

Homework 2 Percolation

截止日期：2024年2月26日​

danger

这次作业可比之前的长多了，跟个小项目似的。所以说，尽早动手！ 已经提醒过你们了。要是搞不定，可别怪没好好理解作业要求，延期是没门的。

常见问题解答​

每个作业开头都有FAQ链接。你也可以在网址后加上“/faq”访问。 作业2的FAQ在这里：此处。

获取初始代码​

请按照作业工作流程指南开始本次作业。本次作业是hw2。

介绍​

这个程序里，我们要用蒙特卡洛模拟来估算渗透阈值。

介绍视频​

作业介绍视频在这里：此链接。视频分三部分：介绍、实现提示和优化提示。想挑战自己的可以忽略提示。 如果你想看Hug教授八年前在普林斯顿做的视频，看这里：此链接。注意：视频里提到要实现PercolationStats.java，但现在我们已经提供完整代码了，不用管那一步。

HW2 幻灯片​

作业幻灯片在这里：此处。因为是作业，不是项目，所以我们放了些解题提示。想挑战自己的可以忽略。

这玩意儿有啥用？​

假设有个混合系统，由随机分布的绝缘和金属材料组成：那要有多少金属材料，系统才能导电？ 再比如，多孔地表有水（或者地下有油），在什么情况下水能渗下去（或者油能冒上来）？ 科学家们用“渗透”这个抽象概念来模拟这些情况。

模型​

我们用N x N的网格模拟渗透系统。每个格子要么是“开放”的，要么是“阻塞”的。“满”格子是指：它本身是开放的，而且能通过一串相邻的（上下左右）开放格子，连到顶行。 如果底行有“满”格子，我们就说系统“渗透”了。 换句话说，把所有能连到顶行的开放格子都填满，如果这过程也填满了底行的某些格子，那系统就渗透了。（比如绝缘/金属材料的例子，开放格子就是金属材料，渗透的系统就是有条从上到下的金属通路，满格子就能导电。 多孔材料的例子里，开放格子就是水能通过的空隙，渗透的系统就是水能从上到下流过去。）

看下面的图，左边的系统里，水能从顶行开始，沿着空格子滴到最下面。 右边的系统，顶行的水就没法滴到最底下了。

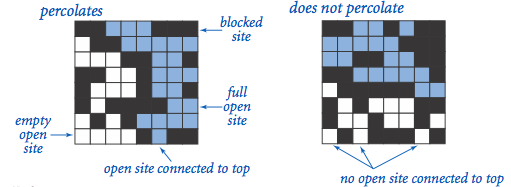
percolates

Percolation.java​

Percolation 类​

为了模拟渗透系统，请完成具有以下API的Percolation类：

public class Percolation {
   public Percolation(int N)                // 创建一个N x N的网格，所有格子初始状态都是阻塞的
   public void open(int row, int col)       // 打开格子(row, col)，如果它还没被打开的话
   public boolean isOpen(int row, int col)  // 格子(row, col)是打开的吗？
   public boolean isFull(int row, int col)  // 格子(row, col)是满的吗？
   public int numberOfOpenSites()           // 已打开的格子数量
   public boolean percolates()              // 系统渗透了吗？
}

渗透问题​

在一个著名的科学问题中，研究人员关注的是：如果每个节点以概率 pp 独立地被设置为开放状态（因此以概率 1−p1 − p 被阻塞），那么该系统发生渗透的概率是多少？当 pp 等于 0 (即所有节点都处于阻塞状态) 时，系统不会发生渗透；当 pp 等于 1 (即所有节点都处于开放状态) 时，系统一定会发生渗透。下图展示了对于 20x20 (左图) 和 100x100 (右图) 随机网格，节点空置概率 pp 与渗透概率之间的关系。

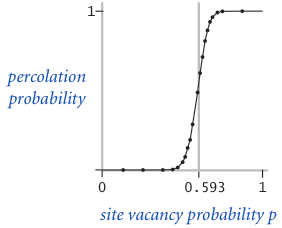
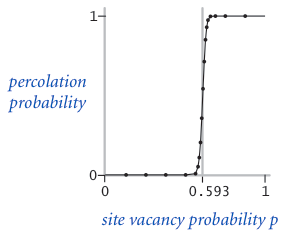
threshold20 threshold100

当 NN 足够大时，存在一个阈值 p^&#42;。当 p < p^&#42; 时，一个随机的 N x N 网格几乎不可能发生渗透；而当 p > p^&#42; 时，该网格几乎必然发生渗透。目前尚未找到确定渗透阈值 p^&#42; 的数学解法。你的任务是编写一个计算机程序来估计 p^&#42;。

info

通过实现上述 API 中给出的所有方法来填写 Percolation.java。

WeightedQuickUnionUF 类​

WeightedQuickUnionUF 类由 Princeton 的 algs4 库提供，并具有以下 API：

public class WeightedQuickUnionUF {
   public WeightedQuickUnionUF(int n)      // creates a UF with n elements
   public int count()                      // number of disjoint sets
   public int find(int p)                  // the root of p's set
   public boolean connected(int p, int q)  // whether p and q are in the same set
   public void union(int p, int q)         // join p and q's sets together
}
danger

务必使用 WeightedQuickUnionUF 类！ 该类已经实现，请勿重新实现 Union Find ADT。

提示与注意事项​

重要提示：我们发布了一系列视频，其中包含有关如何处理此作业的一些提示！请务必观看它们；它们可能会为你节省大量时间。

特殊情况处理​

按照惯例，行和列索引是介于 0 和 N − 1 之间的整数，其中 (0, 0) 是左上角的节点：如果对 open()、isOpen() 或 isFull() 的任何参数超出其规定的范围，则抛出 java.lang.IndexOutOfBoundsException。如果 N ≤ 0，构造函数应抛出 java.lang.IllegalArgumentException。

性能要求​

构造函数的时间复杂度应为 O(N2)O(N^2)；所有其他方法的时间复杂度应为常数级别，加上对 union-find 方法 union()、find()、connected() 和 count() 的常数次调用。满足这些要求有些棘手！你可能会考虑创建一个简单有效的解决方案，然后再想办法使其更快。有关满足速度要求的提示，请参见本规范开头的视频。你的 numberOfOpenSites() 方法必须花费恒定时间。本次作业的目标之一是学习如何将渗透问题转化为一个已解决的问题，即不相交集（也称为 Union Find）问题。

info

如果你已经到了规范的这一部分，但仍然不确定如何开始，请浏览 这些幻灯片并 观看此视频。

PercolationStats.java​

蒙特卡罗模拟。 为了估计渗透阈值，请考虑以下计算实验：

  • 将所有节点初始化为阻塞状态。
  • 重复以下步骤，直到系统发生渗透：
    • 在所有阻塞的节点中，均匀随机地选择一个节点。
    • 打开该节点。
  • 当系统发生渗透时，已打开节点所占的比例可以作为渗透阈值的估计值。 例如，如果按照下方快照所示，在一个 20x20 的网格中随机打开一些格点，当打开第 204 个格点时系统发生渗透，那么我们估计的渗透阈值为 204/400 = 0.51。 这些图片分别展示了打开 50 个、100 个、150 个以及 204 个格点时的状态。

percolation50 percolation100 percolation150 percolation204

如果您对以下计算背后的数学原理感兴趣，请点击此处。

通过重复此计算实验 TT 次并对结果进行平均，我们可以获得更准确的渗透阈值估计值。 设 x_tx\_t 为计算实验 tt 中开放格点的比例。 样本均值 μ\mu 提供了渗透阈值的估计值；样本标准差 σ\sigma 衡量了阈值的离散程度。

μ=x_1+x_2+...+x_TT\mu = \frac{x\_1 + x\_2 + ... + x\_T}{T}, σ2=(x_1−μ)2+(x_2−μ)2+...+(x_T−μ)2T−1\sigma^2 = \frac{(x\_1 - \mu)^2 + (x\_2 - \mu)^2 + ... + (x\_T - \mu) ^2}{T-1}

假设 TT 足够大（例如，至少为 30），则以下公式提供了渗透阈值的 95% 置信区间：

[μ−1.96σT,μ+1.96σT][\mu - \frac{1.96\sigma}{\sqrt{T}}, \mu + \frac{1.96\sigma}{\sqrt{T}}]

为了执行一系列计算实验，我们为您提供了一个 PercolationStats 数据类型。

构造函数接受两个参数 N 和 T，并在一个 NxN 的网格上进行 T 次独立的计算实验（如前所述）。 使用此实验数据，它计算渗透阈值的平均值、标准差和 95% 置信区间。

info

打开 PercolationStats.java 并查看提供的构造函数和方法。 然后，运行 main 方法并解释结果。 这些数字告诉您关于渗透问题的解决方案什么信息？

本部分作业无需提交任何内容；如果 Percolation.java 实现正确，您应该能够得到渗透阈值 p 的 95% 置信区间。

运行时分析（未评分）​

此部分作业不会被评分，但强烈建议您至少阅读并思考以下几点：

  • 使用 QuickFindUF 中的快速查找算法实现 Percolation 数据类型。 使用 Stopwatch 测量 PercolationStats 在不同 N 和 T 值下的总运行时间。 将 N 加倍如何影响总运行时间？ 将 T 加倍如何影响总运行时间？

  • 现在，使用 WeightedQuickUnionUF 中的加权快速联合算法实现 Percolation 数据类型。 回答上一个要点中的相同问题。

提供的文件​

我们提供了两个客户端程序，可以用来进行大规模的可视化追踪。 我们强烈建议您使用它们来测试和调试您的 Percolation 实现。

示例数据文件​

inputFiles 目录包含一些用于可视化客户端的示例文件，包括 input20.txt，我们将在下面使用它。

此处 是与每个输入文件对应的预期输出图像。

基于文件的可视化客户端​

PercolationPicture.java 通过执行以下步骤进行可视化：

  • 从文件中读取网格大小 N。
  • 创建一个 N x N 的格点网格（最初全部被阻塞）。
  • 从文件中读取一系列需要打开的格点的坐标（行 i，列 j）。 在每个格点打开后，使用标准绘图以浅蓝色绘制完整格点，以白色绘制开放格点（非完整格点），以黑色绘制阻塞格点，其中格点 (0, 0) 位于左上角。

对于输入文件 input20.txt，该程序应生成如下图所示的输出。 这些图像分别对应于 50、100、150、204 和 250 个格点被打开的情况。

percolation50 percolation100 percolation150

percolation204 percolation250

你可以通过在 IntelliJ 中，依次点击“运行 -> 编辑配置 -> + -> 应用程序”，并在其中设置正确的参数，来运行此输入对应的可视化工具。 在配置中，将“主类”设置为 PercolationPicture，并将“程序参数”设置为输入文件，例如 inputFiles/input20.txt。 最后，点击“运行”按钮即可开始运行可视化工具。

info

打开 PercolationPicture.java 并按照上述步骤运行可视化工具。 使用此工具来帮助你调试 Percolation.java 方法！

交互式可视化客户端​

InteractivePercolationVisualizer.java 通过鼠标输入，以动画方式展示在渗透系统中打开网格单元的结果。 它接受一个命令行整数 N，用于指定网格的尺寸。 此外，它还会以与上述 PercolationPicture 相同的格式，打印出已打开网格单元的序列。因此，你可以利用它来生成有趣的测试文件。 如果你创建了有趣的数据文件，欢迎在 Ed 上分享。

info

打开 InteractivePercolationVisualizer.java 并按照与 PercolationPicture 相同的步骤运行交互式可视化工具。 请注意，对于交互式版本，你不需要提供程序参数。

使用此工具来帮助你调试 Percolation.java 方法！

注意：如果你使用的是 IntelliJ，你可以在“运行 -> 编辑配置”中选择要运行的类 (即选择要运行的主方法)。 更多信息请参考 FAQ。

测试​

你会发现 InteractivePercolationVisualizer 对于验证 Percolation 类的实现是否正确非常有帮助。 如果你的实现正确，单击单元格应该会打开这些单元格 (并在必要时进行填充)。 还会显示已打开单元格的数量，以及系统是否渗透的提示信息。

我们在 tests 文件夹中提供了两个基本测试。 你应该在 PercolationTest.java 中添加更多测试来验证你的代码。

提交 & 交付​

你应该以通常的方式提交，即推送到 GitHub，然后在 Gradescope 上提交。 此作业没有速度限制。

交付内容：

  • Percolation.java

致谢​

此作业最初由 Kevin Wayne 和 Bob Sedgewick 在普林斯顿大学开发，自动评分器由 Josh Hug 为普林斯顿算法课程构建。