Skip to main content

Lab 05 Disjoint Sets

常见问题页面​

请参考我们的常见问题页面。本周我们会持续更新网站上的常见问题页面！

介绍​

今天，我们将深入探讨不相交集。我们强烈建议您在开始本次实验前观看关于不相交集的讲座。讲座内容涵盖了实验入门所需的知识。

本周的实验中，我们将实现自定义的不相交集UnionFind，具体来说，是实现加权快速合并 + 路径压缩。

更多信息请参考讲座。

从骨架中拉取文件：

git pull skeleton main

不相交集​

作为回顾，让我们介绍一下什么是不相交集。不相交集数据结构表示一组互不相交的集合，即该数据结构中的任何元素都只属于一个集合。

对于不相交集，我们主要关注两个操作：union 和 find。 union 操作会将两个集合合并为一个集合。 find 操作将接收一个元素，并告诉我们该元素属于哪个集合。 通过这些操作，我们可以方便地检查两个元素是否相连。

快速合并​

正如讲座中介绍的，我们讨论了快速合并。在这种表示方法下，我们可以将不相交集数据结构看作一棵树。 具体来说，这棵树将具有以下特性：

  • 节点将是我们集合中的元素，
  • 每个节点只需要指向其父节点的引用，而不是直接指向集合本身。每棵树的顶部（我们称之为“根”）代表了它所代表的集合。

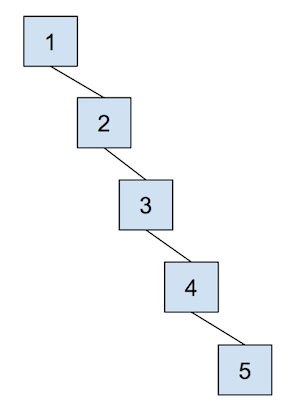
然而，这种方法的一个问题是，union操作在最坏情况下的运行时间是线性的，这取决于元素的连接方式。换句话说，树可能会变得很高，导致union操作的性能下降。 例如，请看下面的例子，思考一下为什么这会导致最坏情况的运行时间？

worst

现在，让我们通过以下优化来克服此数据结构的缺点。

加权快速合并​

我们对快速合并数据结构进行的第一个优化叫做“按大小合并”。 这样做是为了尽可能地降低树的高度，避免出现导致最坏情况运行时间的细长树。 当我们对两棵树进行union操作时，总是将较小的树（节点数较少的树）作为较大树的子树。如果大小相同，则可以任意选择。我们称之为加权快速合并。

因为我们使用了“按大小合并”策略，所以任何元素的最大深度都将是O(log⁡N)O(\log N)，其中NN是数据结构中存储的元素数量。相比于未优化的快速合并的线性时间复杂度，这是一个很大的提升。

简单来说，元素xx的深度只有在其所在的树T1T_1被合并到另一棵树T2T_2下时才会增加。 此时，合并后的树的大小至少是T1T_1的两倍，因为size(T2)≥size(T1)size(T_2) \ge size(T_1)。 因此，最初只包含xx的树最多可以翻倍log⁡N\log N次，直到包含NN个元素。

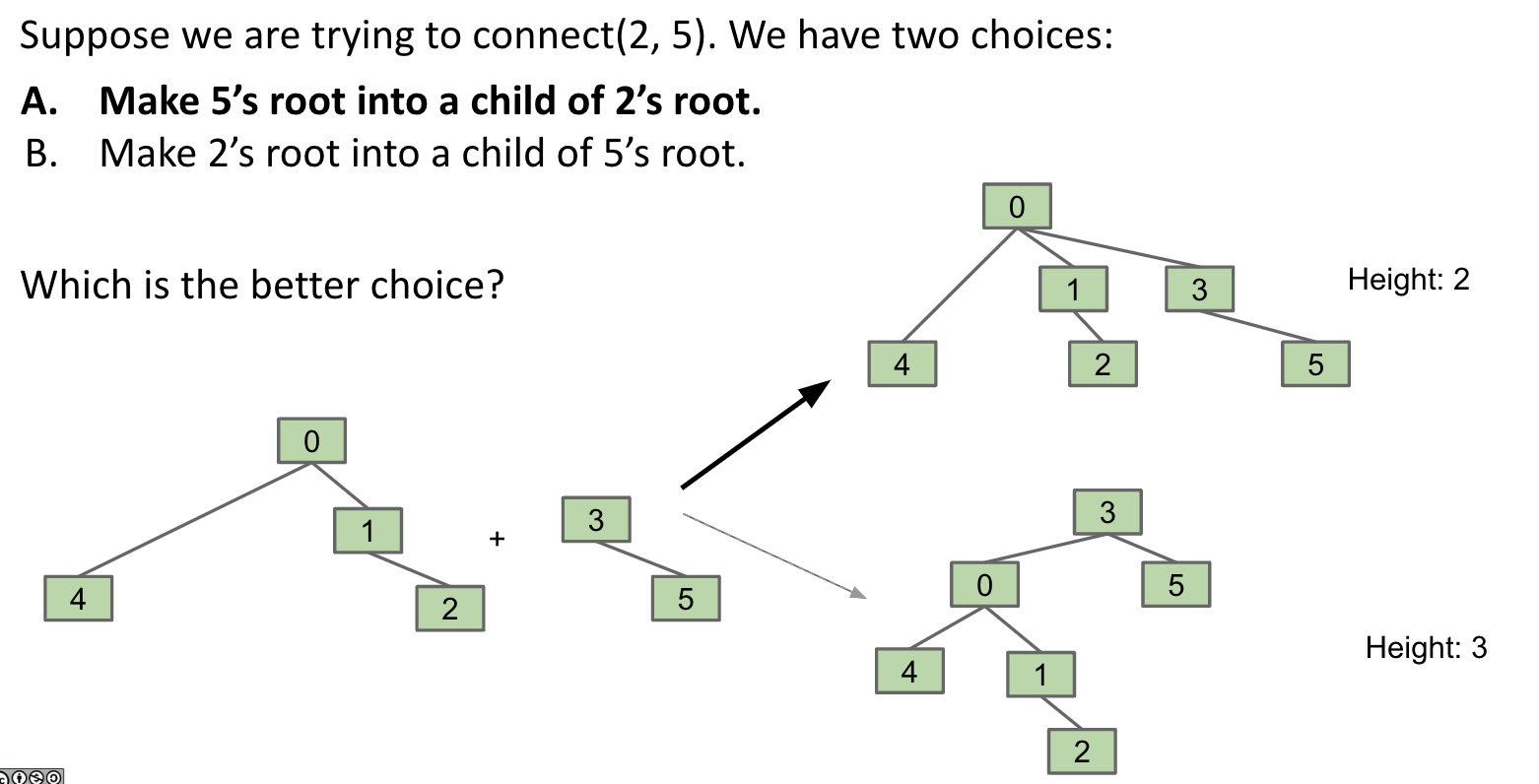
请参考以下示意图，以便更好地理解其工作原理： Weighted Quick Union

例子​

danger

本例中，当两棵树大小相同时，选择最小的元素作为根节点。请注意，这取决于具体的实现方式。

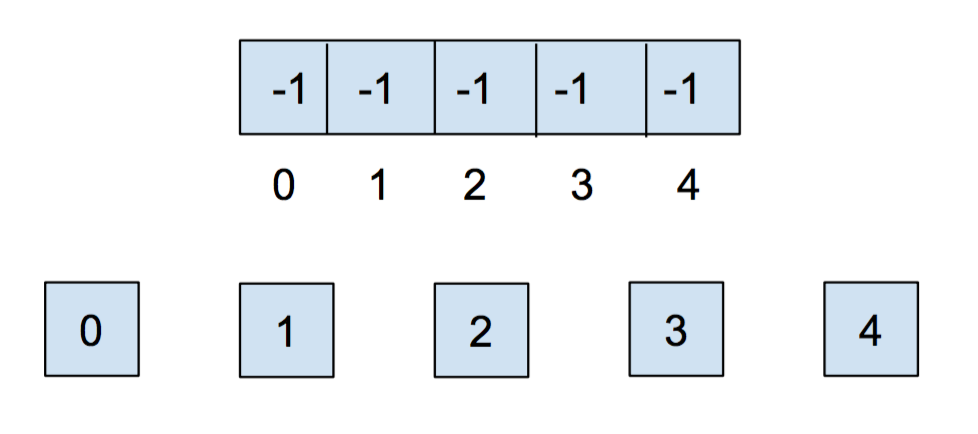
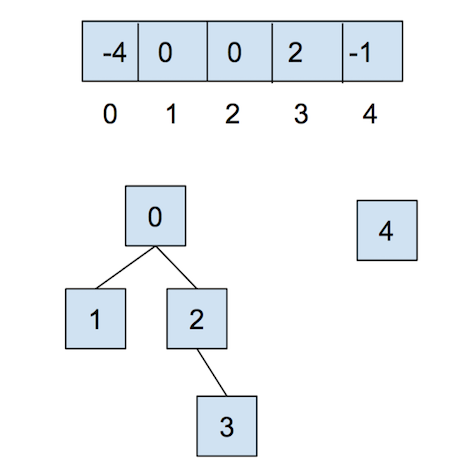
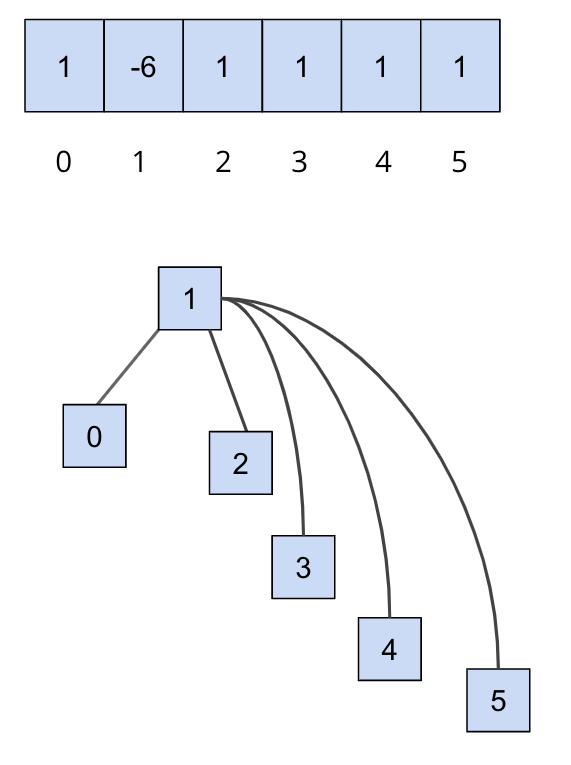
让我们通过一个例子来理解加权快速合并。 在初始化不相交集时，每个元素都属于独立的集合，因此我们将数组中的所有元素初始化为-1。 为了跟踪集合的大小，我们将集合的权重以负数的形式存储在其根节点上（-weight），以此来区分父节点和集合的权重。

initial

在我们调用 union(0,1) 和 union(2,3) 之后，我们的数组和我们的抽象表示将如下所示

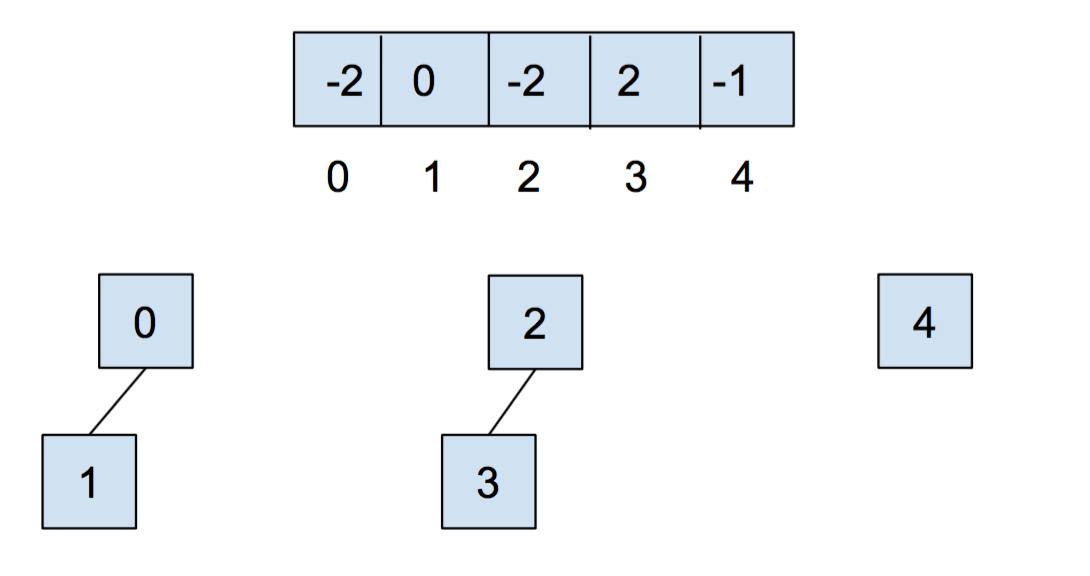union1 请注意，在上面的例子中，索引0和2对应的值都是-2，这是因为每个集合的根节点存储的是其大小的相反数。现在，如果我们调用 union(0,2)，结果会是这样：

union2

为了方便理解，我们假设有另一个并查集，当前状态如下图所示（沿用之前的平局打破策略）：

wqu1

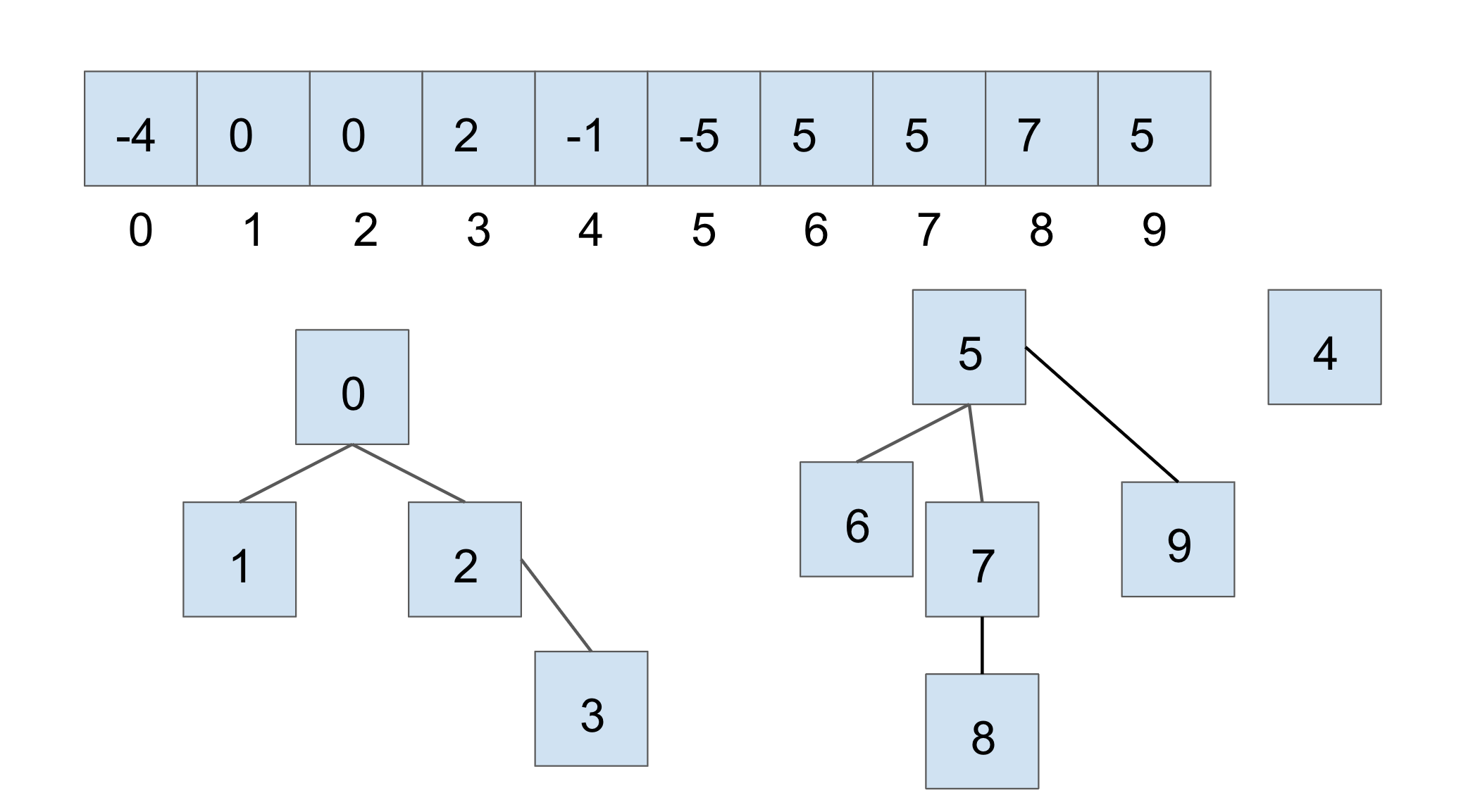
如果我们执行 union(7, 2) 来合并这两个较大的集合，结果如下：

wqu2

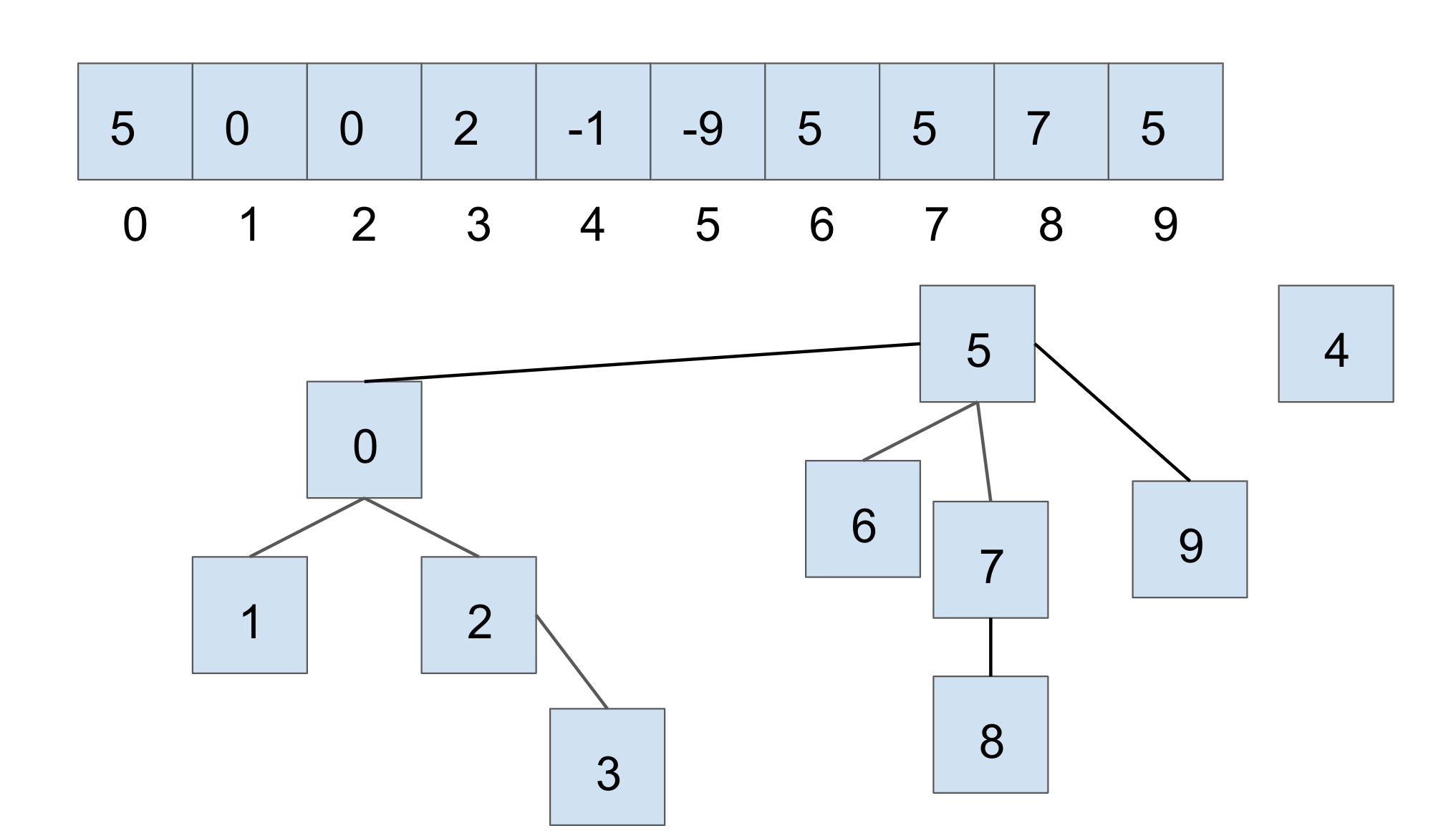
在这种情况下，我们将索引7和2所在集合的根节点连接起来，较小集合的根节点会成为较大集合根节点的子节点。在使用加权快速联合算法时，我们需要更新数组中的两个值：

  • 将较小集合的根节点的父节点指向较大集合的根节点
  • 相应地更新较大集合根节点的值，以反映新的集合大小

路径压缩​

即使我们已经通过加权快速联合这种数据结构实现了加速，仍然有进一步优化的空间！如果我们有一棵很深的树，并且重复地在最底层的叶子节点上调用 find 方法，会发生什么？每次调用，我们都必须从叶子节点到根节点遍历整棵树。

一个巧妙的优化方法是将叶子节点向上移动，使其直接成为根节点的子节点。这样，下次您在该叶子节点上调用 find 方法时，它将运行得更快。更进一步，我们可以对从叶子节点到根节点的路径上的所有节点都执行相同的操作。具体来说，当我们对某个元素调用 find 方法时，所有在向上追溯到根节点的路径上经过的节点都会被更新，直接指向根节点。这种优化称为路径压缩。一旦找到某个元素，路径压缩就能使后续查找该元素（以及路径上所有节点）的速度大大提升。

对于任何 ff 次 find 操作和 uu 次 union 操作的组合，其运行时间为 Θ(u+fα(f+u,u))\Theta(u + f \alpha(f+u,u))，其中 α\alpha 是一个增长极其缓慢的函数，称为 反阿克曼函数。这里的“运行时间”指的是执行这些操作所需的时间复杂度。之所以说“增长极其缓慢”，是因为在实际应用中，对于通常会遇到的输入规模，反阿克曼函数的值几乎都不会超过4。这意味着，在实际应用中，带有路径压缩的加权快速联合数据结构的 find 操作平均可以在常数时间内完成！

重要的是要注意，即使对于所有实际大小的输入，此操作都可以被认为是常数时间，我们也不应将整个数据结构描述为常数时间。 我们可以说，对于小于某个非常大尺寸的所有输入，它将是常数。 如果没有该限定，我们仍然应该使用反阿克曼函数来描述它。

下面显示了一个用于演示路径压缩效果的例子。我们从以下结构开始：

danger

这只是一个用于演示路径压缩效果的例子。 请注意，您无法使用加权快速联合获得此结构（第一张图片，正下方）。

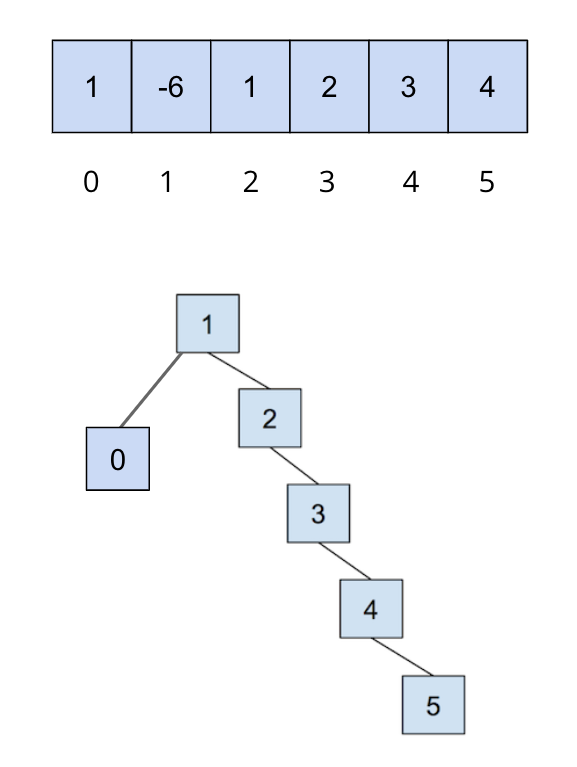
path_compression_before

在执行 find(5) 之后，所有为了找到根节点而遍历过的节点都会被更新，直接指向根节点：

path_compression_after

您可以访问此链接 here 来玩转并查集。

练习：UnionFind​

info

在 UnionFind 的实现中，您需要完成带有路径压缩的加权快速联合算法。

接下来，我们将要实现我们自己的不相交集数据结构，UnionFind。如果你还没有看过 UnionFind.java 文件，请先查看。文件中已经提供了一些框架代码，你需要完成以下方法的实现：

  • UnionFind(int N)：这是构造函数。它创建一个 UnionFind 数据结构，它能容纳 N 个项目。
  • int sizeOf(int v)：返回 v 所属集合的大小。
  • int parent(int v)：返回 v 的父节点。
  • boolean connected(int v1, int v2)：如果两个顶点已连接，则返回 true。
  • int find(int v)：返回 v 所属集合的根。
  • void union(int v1, int v2)：将 v1 和 v2 连接在一起。

我们建议你从实现构造函数开始，并在实现其余方法之前先查看 find。

:::task 完成 UnionFind 中的方法。你需要在 union 中使用 find。 :::

实验注意事项​

请注意，在本实验中，我们将使用非负整数作为不相交集中的项目。

每个方法都提供了注释，并且会比上面的摘要更详细，因此请务必仔细阅读这些注释，以了解你需要实现的内容。请记住实现上面讨论的两种优化，并注意某些方法的注释中描述的平局处理机制。

danger

对于本实验，你需要实现以下平局处理机制：如果集合的大小相等，将 v1 的根节点连接到 v2 的根节点，以此来打破平局。

你还应该正确处理错误的输入，例如，如果将无效顶点传递给函数，则抛出 IllegalArgumentException。你可以使用以下行抛出 IllegalArgumentException：

throw new IllegalArgumentException("Some comment to describe the reason for throwing.");

测试​

danger

对于本实验，我们提供了一些测试供你检查你的实现，但它们并不全面。本地只提供了自动评分器上6个测试中的4个。在本地通过测试并不意味着你将通过 Gradescope 上的测试，你需要编写自己的测试来验证正确性。

如果你发现自己未通过最后两个测试，请确保你已正确实现了路径压缩，并且你已测试了你所实现的所有方法是否正确。

提交​

像之前的作业一样，添加 (add)、提交 (commit)，然后将你的 Lab 05 代码推送到 GitHub。然后，提交到 Gradescope。

  • 完成 UnionFind.java 的实现。此实验总共占 5 分。