Lab 07 LLRBs
常见问题解答
本实验的常见问题解答可以在这里找到。
准备工作
像往常一样,从 skeleton 拉取 Lab 07 的文件,然后在 IntelliJ 中打开。
学习目标
在本实验中,我们将实现左倾红黑树。
介绍
在之前的实验中,我们分析了用于访问和插入二叉搜索树的算法的性能。 然而,在某些情况下,我们总是假设树是平衡的 - 正如我们所见,可能会产生一棵倾斜的树,从而影响我们数据结构的性能。
非正式地,树“平衡”意味着从根到每个叶子的路径长度大致相同。 任何需要遍历树的每一层的算法,例如二叉搜索树的查找,其时间复杂度都取决于层数。 关于二叉搜索树,我们可以拥有的最小层数是关于节点数的对数(即 )。
为了保持“平衡”的这种特性,我们希望防止获得“倾斜”树的最坏情况,这会导致更差的性能时间。 因此,平衡搜索树/B 树应运而生。它们能够自平衡,从而保持我们期望的“平衡”特性。
但是,在本实验中,我们将不专注于实现平衡搜索树 - 为什么? 虽然它们能保证从根节点到任意叶节点的路径长度为 ,但其代码实现难度较高,较为繁琐,并且在常见操作中存在很多边界情况。 它们仍然被普遍使用并提供了很多好处,但它们确实有缺点。 请注意,在本实验中,我们提到的平衡搜索树均指 2-3 树。
接下来,我们将学习一种相关的数据结构:左倾红黑树。 我们建议您在开始本实验之前查看相关的讲座幻灯片。
链接 vs 节点
请不要跳过本节。 在继续本实验之前,请务必阅读本节。 如果你不阅读本节,你将会感到更加困难。
在讲座中,我们介绍了使用链接的 LLRB 的概念。 但是,对于本实验,我们将不使用链接来表示我们的 LLRB。 相反,我们将使用节点。 主要原因是基于链接的实现远比基于节点的实现要复杂。 为了更好地理解,请参考以下示例,它展示了我们在讲座中是如何对该概念进行可视化的。
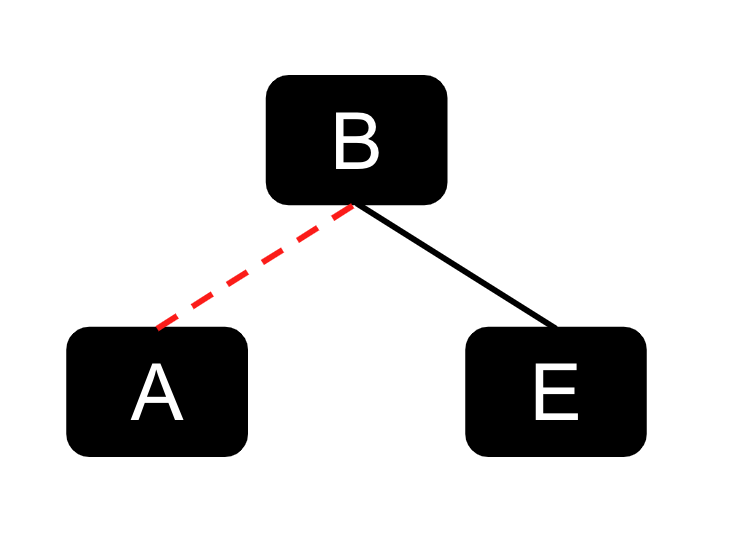
对于本实验,由于我们将处理着色节点 - 红色链接与其连接的节点之间的关系可以定义如下:
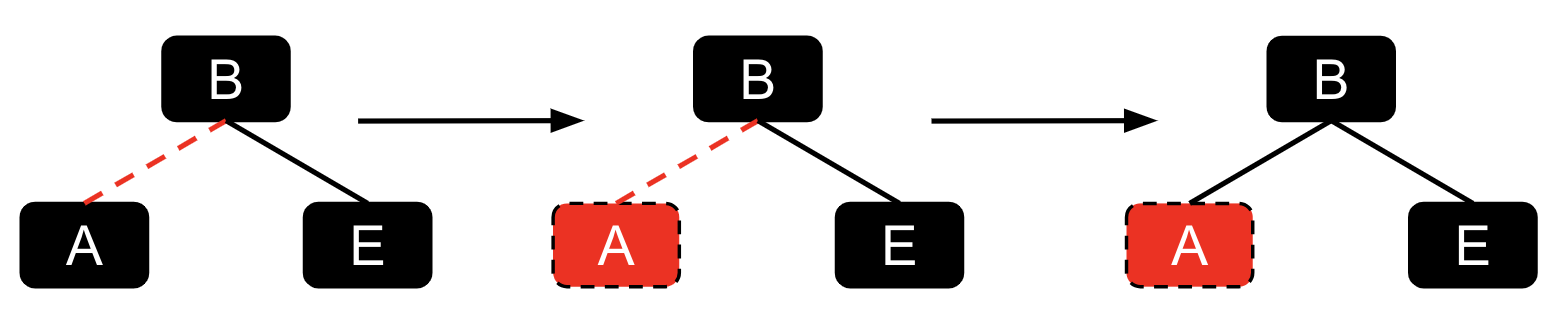
最初,A 通过红色链接连接到 B。 但是,如果我们在表示中使用着色节点而不是链接,则 A 本身将被着色为红色。 上面的可视化是为了说明红色链接与着色节点之间的对应关系,请在后续实验中牢记这一点!
请务必理解着色链接和着色节点之间的关系。在后续的示例和描述中,我们将使用着色节点,以便简化实验的实现。
左倾红黑树
本质上,LLRB树就是一种二叉搜索树,但它增加了一些约束条件,即每个节点需要被“着色”为红色或黑色。这种“着色”在2-3树和LLRB树之间建立了一种一一对应的关系!也就是说,每一棵2-3树都唯一对应于一棵LLRB树,反之亦然。
这种对应关系非常有用:LLRB树不仅继承了二叉搜索树的所有基本操作,还通过额外的维护工作,实现了与2-3树相同的平衡性。
LLRB树的特性
现在我们来详细说明 LLRB 树的一些特性。 特别是,我们使用有效的 LLRB 树和 2-3 树之间的一一对应关系来推导出这些特性。
使用彩色节点作为我们的表示,根节点必须涂成黑色。 : 我们将红色节点视为与其父节点位于同一个2-3节点中。 由于根节点没有父节点,所以它不能是红色的。
如果一个节点有一个红色子节点,它必须在左边。 : 这保证了树的左倾性。
任何节点都不能同时拥有两个红色的子节点。 : 如果一个节点有两个红色子节点,则意味着这三个节点(父节点和两个子节点)位于同一个2-3节点中。 这意味着对应的2-3节点包含了3个键,这是不允许的。
红色节点不能有红色的父节点(即红色节点的父节点必须是黑色的)。 : 如果一个红色节点有一个红色父节点,那么红色子节点和红色父节点都与红色父节点的父节点位于同一个 2-3 节点中。 这意味着对应的2-3节点包含了3个键,这是不允许的。
在平衡的LLRB树中,从根节点到任何空引用的路径上,黑色节点的数量都是相同的。 : 在平衡的 2-3 树中,每个空节点与根节点的距离相同。 我们知道,LLRB树中的每个黑色节点都对应于等价的2-3树中的一个节点。 因此,从LLRB树的根节点到任何空节点的路径上,黑色节点的数量都是相同的。
插入 LLRB 树
向LLRB树中插入节点的过程,首先与标准的二叉搜索树插入算法相同,即通过搜索找到合适的叶子节点位置。
无论何时向LLRB树中插入新节点,该节点都会被着色为红色。
然而,插入新节点后,可能会破坏LLRB树的约束条件,因此我们需要额外的操作来“恢复”这些特性。 我们知道有效的 LLRB 树与 2-3 树之间存在一一对应关系。 让我们使用这种对应关系来尝试推导出这些操作。
接下来,我们将讨论哪些情况会导致约束条件被破坏,以及如何通过相应的操作来修复它们。
约束条件:如果一个节点有一个红色子节点,它必须在左边
正如前面提到的,新插入的节点总是红色的。 假设我们将新节点插入到LLRB树中,并且该节点最终成为了节点“a”的右子节点(这意味着新节点的值大于“a”)。 假设节点“a”的左子节点是黑色的,或者根本不存在。 这违反了“如果一个节点存在红色的子节点,那么该子节点必须是左子节点”这一约束条件。 为了避免出现向右倾斜的红色连接,我们需要在父节点上执行左旋操作。 如下图所示:
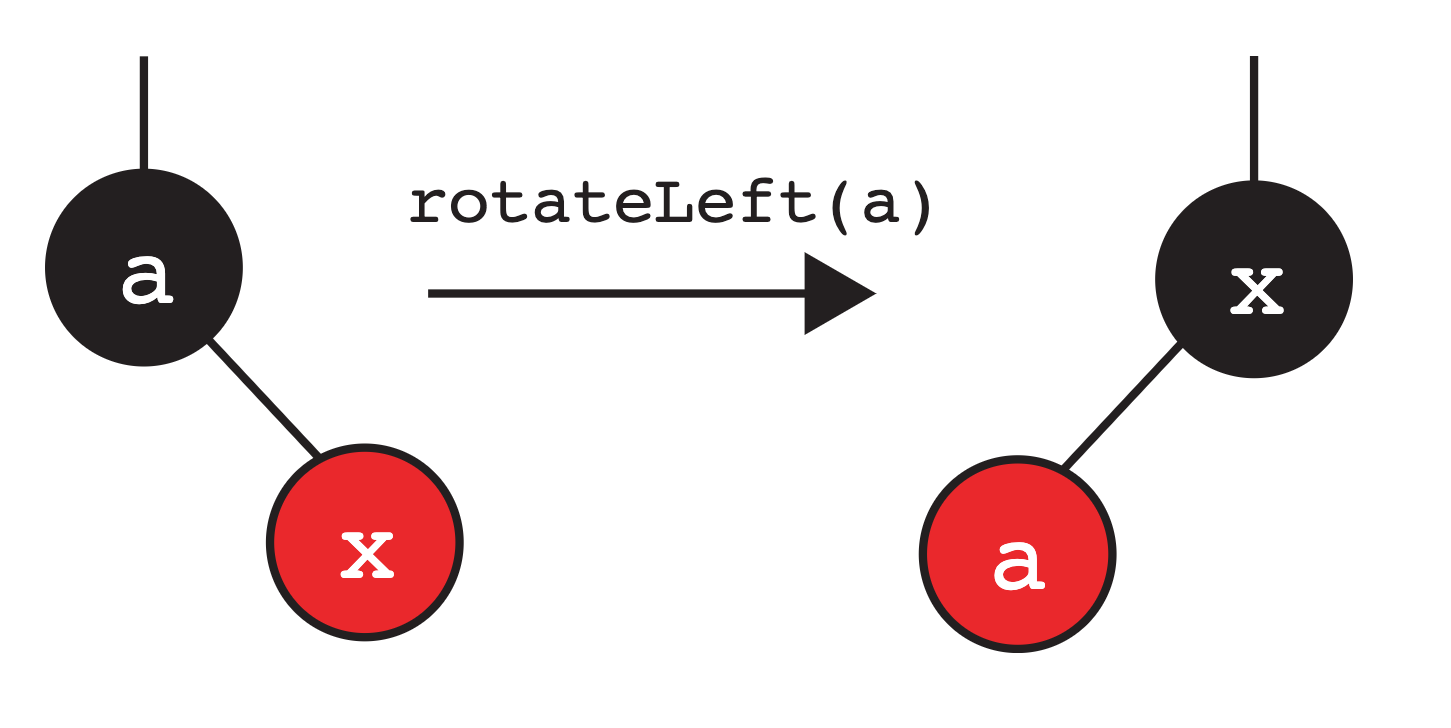
约束条件:任何节点都不能同时拥有两个红色的子节点
让我们考虑另一种情况。与前面类似,我们将一个新节点作为红色节点插入LLRB树中,并且假设它最终成为了节点b的右子节点(在本例中)。那么,如果节点b的左子节点也是红色节点,会发生什么呢? 这就违反了“任何节点都不能有两个红色子节点”的规则。 接下来,我们需要对其父节点执行“颜色翻转”操作。具体来说,我们对节点b进行颜色翻转,即同时翻转节点b及其子节点的颜色。
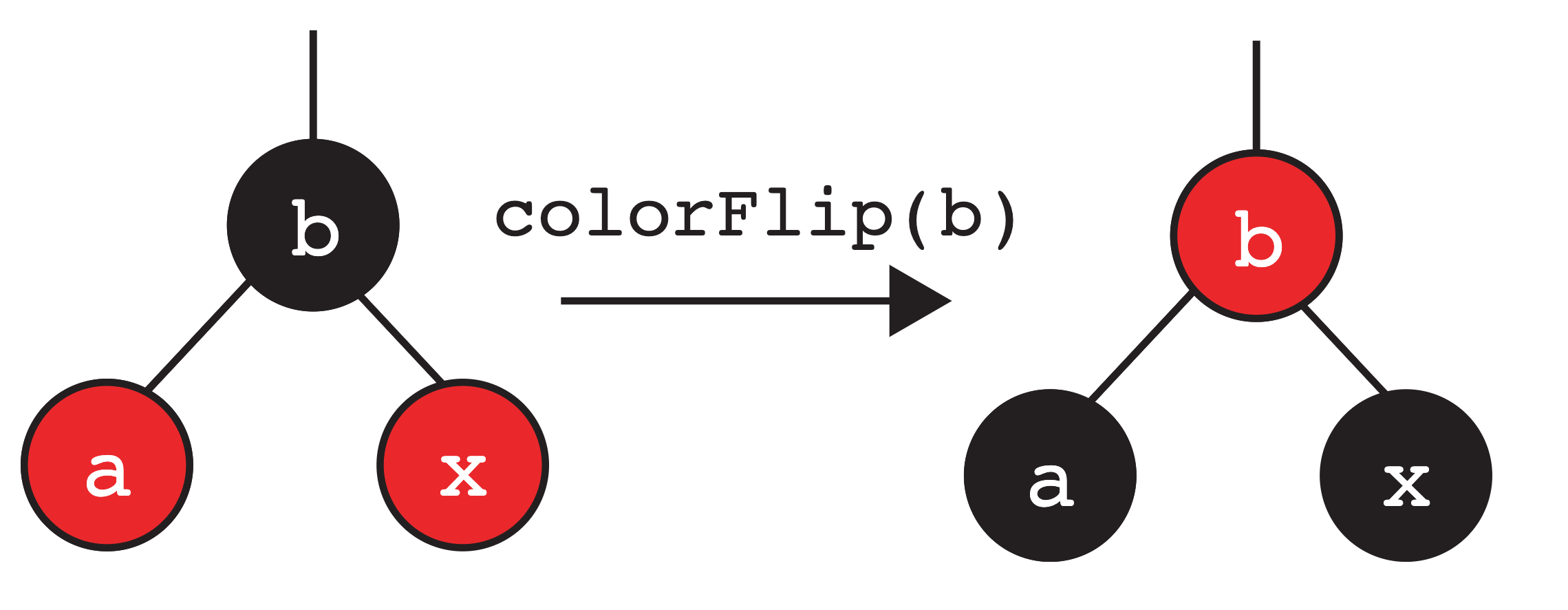
我们稍后会回到这个配置。
规则:红色节点不能有红色的父节点(即,红色节点的父节点必须是黑色)
这可以分解为以下定义的两种情况。
两个连续左倾的红色节点。
如果我们插入的新节点成为了一个红色节点的左子节点,会发生什么呢? 此时,我们需要调整操作,进行“右旋”(也就是说,不能存在两个连续左倾的红色节点)。
右旋是左旋的逆操作! 如果将右旋应用于新的根节点,它会将我们带回到最初的子树结构。
在这种情况下,我们对 b 进行右旋:
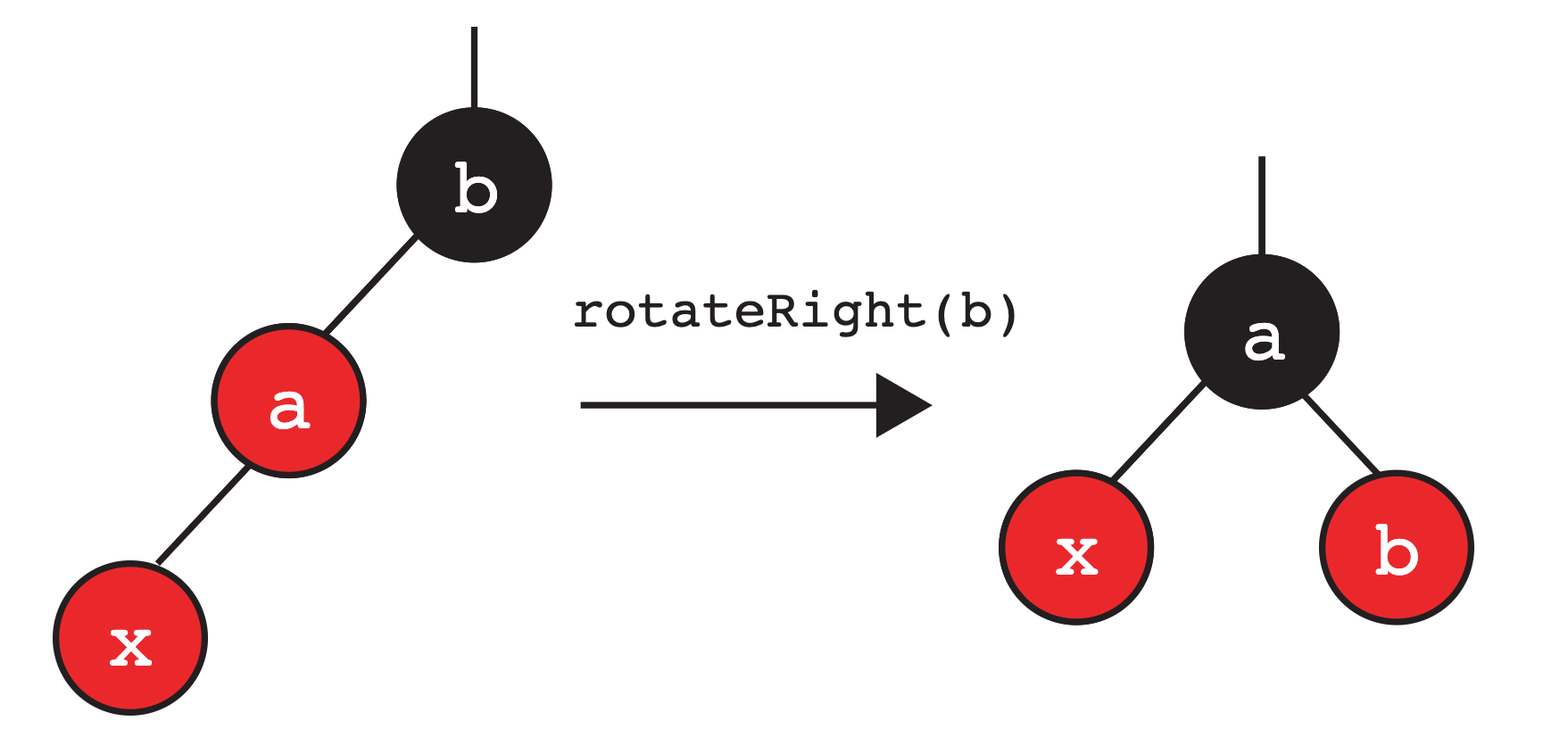
此时,我们注意到它与前一种情况相同,因此我们对 a 应用颜色翻转。
具有右倾红色子节点/节点的红色节点。
另一种情况是,我们插入的新节点可能最终成为一个已是红色节点的节点的右子节点。 此时,我们需要执行左旋操作。
如下图所示,我们在此示例中对 a 进行左旋,得到:
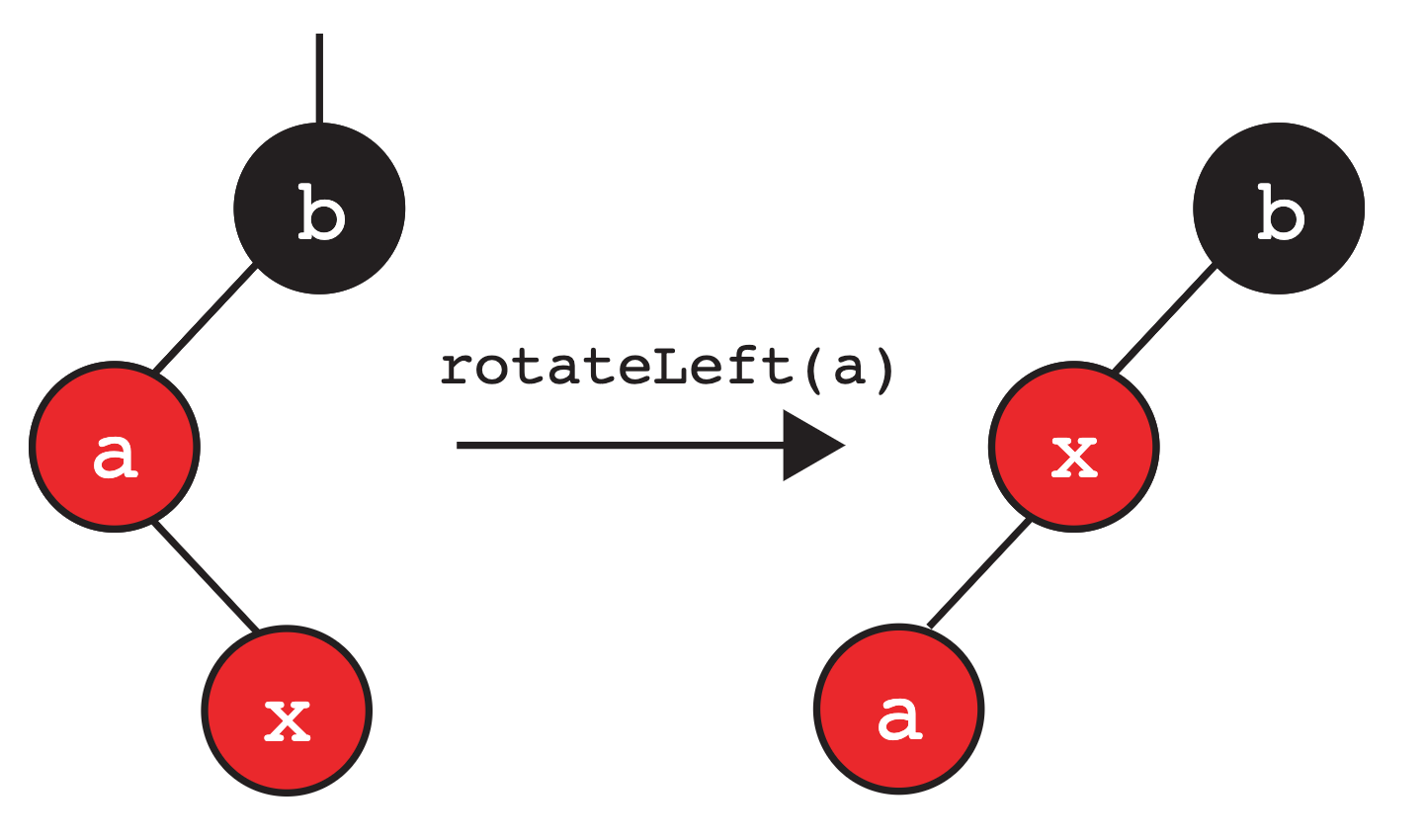
请注意,这与前面提到的规则相符,即不能存在红色右倾的节点。 此时,情况又回到了之前讨论过的状态,因此我们可以对节点b进行右旋,并对根节点x执行颜色翻转。
向上冒泡
等等——请注意,我们刚刚介绍的某些情况最终导致了颜色翻转。 如果我们修改的子树是一个右子树,并且树的其余部分看起来像这样,该怎么办:
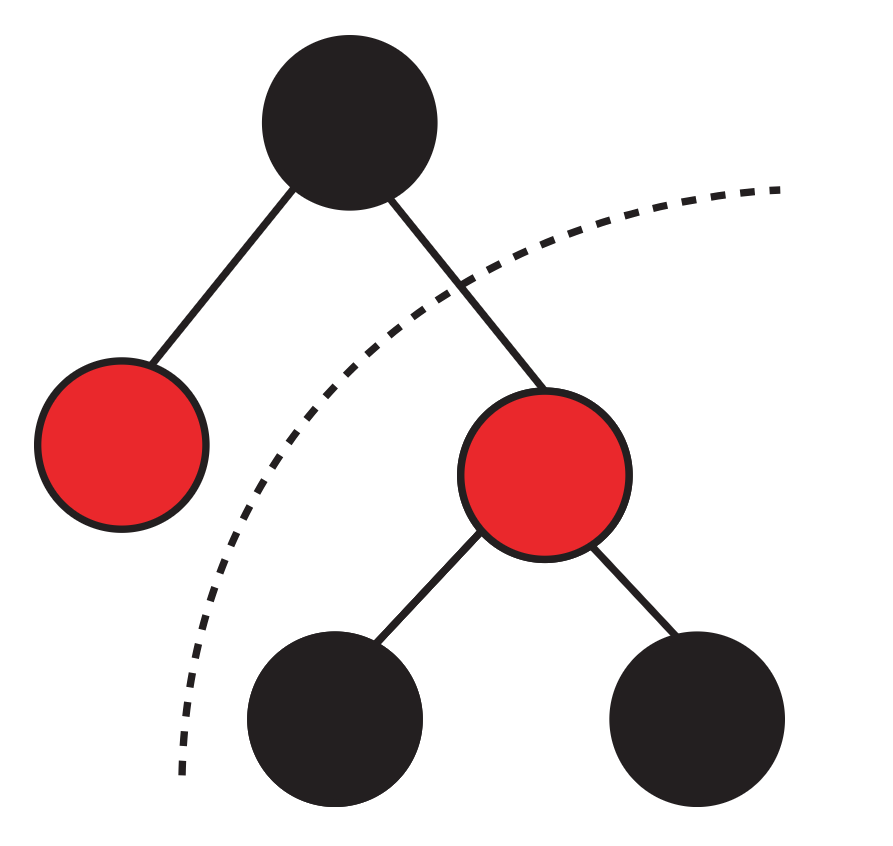
正如在2-3树中向上移动键可能导致父节点溢出一样,执行这些变换也可能会违反LLRB树的规则,从而导致我们再次遇到上述三种情况之一。 我们解决这些情况,直到:
- 没有任何违反的规则
- 翻转根的颜色
这意味着,执行颜色翻转、右旋或左旋等操作后,可能会破坏其他的规则,进而需要进行更多的调整。 在尝试解决这些问题时,这些变换会有效地在LLRB树中向上进行,直到所有规则都满足为止。
另外,在某些情况下,我们必须记得将根节点恢复为黑色。
LLRB 插入摘要
本节内容对于完成实验非常有帮助,您可以参考下面的图示来理解如何执行这三种操作。 请思考如何将旋转和颜色翻转操作转化为节点和指针重新赋值的问题。
我们讨论了三种操作,可以在插入节点后用来“修复”LLRB树的不变性。因为如上所述,可能存在向上渗透的情况,因此,让我们尝试更直观地概括这些操作,特别是旋转操作。
这两种旋转操作可以将右子节点或左子节点提升到父节点的位置。
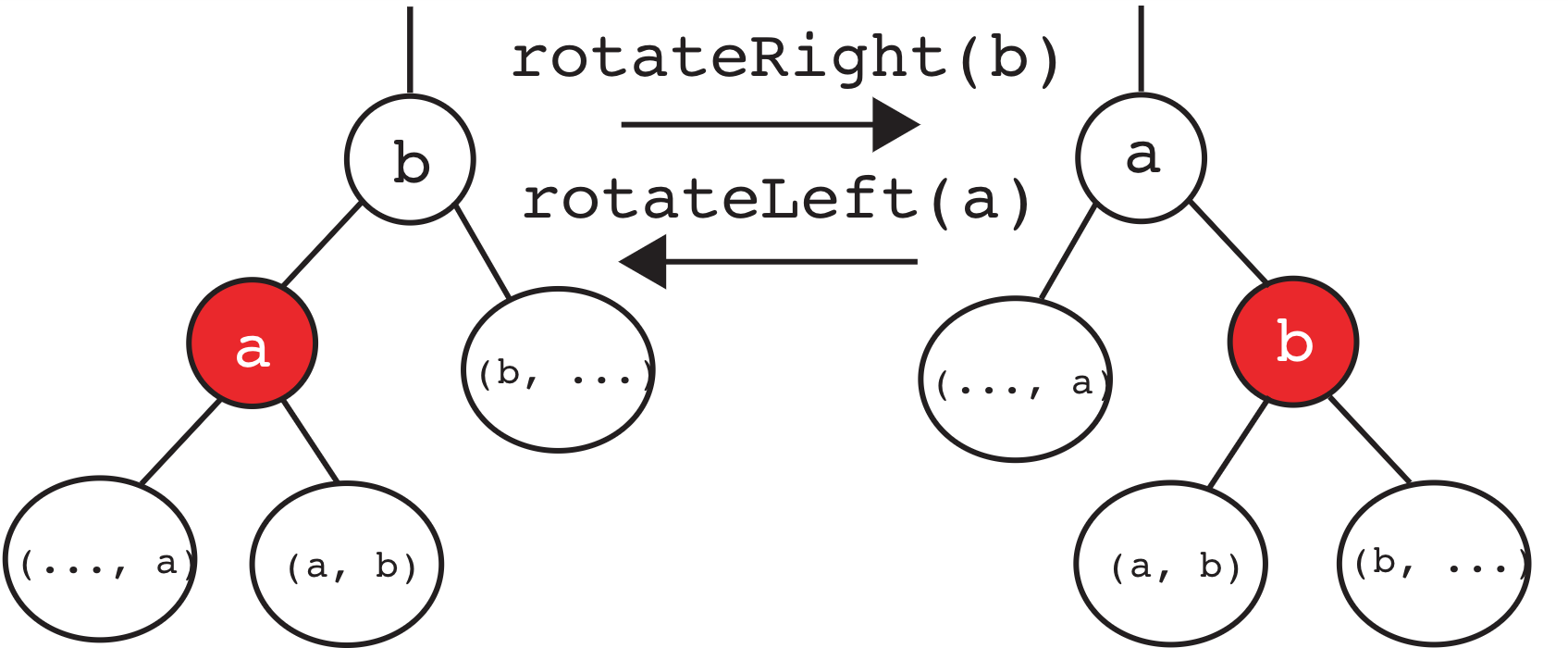
以下是简要描述当我们 rotateRight(b) 时会发生什么:
- 子树的根已从
b更改为a了。 a和b向右移动了。- 两个节点交换颜色,以便新根与旧根的颜色相同了。
- 重组后的子树仍然满足二叉搜索树的属性了。
以下是简要描述当我们 rotateLeft(a) 时会发生什么:
- 子树的根已从
a更改为b了。 a和b向左移动了。- 两个节点交换颜色,以便新根与旧根的颜色相同了。
- 重组后的子树仍然满足二叉搜索树的属性了。
我们还有颜色翻转操作:

LLRB 树的实现
您是否已经阅读了链接与节点这一节? 如果还没有,请务必在开始实验前阅读。
在开始之前,请务必通读整个类 RedBlackTree.java,尤其是提供的嵌套节点类。 确保也阅读每种方法的注释!
练习:颜色翻转
让我们首先考虑颜色翻转操作,这对于 LLRB 树的实现至关重要。 给定一个节点,此操作只需翻转其颜色和子节点的颜色。
在 RedBlackTree.java 中实现 flipColors 方法。
练习:旋转
我们已经看到,我们可以旋转树来平衡它,而不会违反二叉搜索树的不变量。 现在,我们将自己实现它!
对于您的实现,请确保交换旧根和新根的颜色!
提示:这两个操作是对称的。
代码差异会很大吗? 如果您发现自己陷入困境,请查看上面显示的示例!
在 RedBlackTree.java 中,实现 rotateRight 和 rotateLeft。
练习:insert
我们现在将在 RedBlackTree.java 中实现 insert。 我们为您提供了一些带有注释的逻辑结构。 insert 方法的第一部分应该实现标准的二叉搜索树插入。 接下来,您需要处理可能触发 rotateLeft、rotateRight 和 colorFlip 操作的各种情况。 请务必仔细遵循每种情况下的步骤!
请务必使用您已经实现的方法(rotateRight、rotateLeft、flipColors)来简化代码编写。
辅助方法 isRed 已经在骨架代码中提供给您,因此请确保使用它!
在 RedBlackTree.java 中实现 insert 方法。
测试
所有测试都已在本地提供给您。 如果您通过 TestRedBlackTree.java 中的所有测试,您将在 Gradescope 上获得全部学分。 测试代码中包含注释,以帮助您进行调试。
需要完成的内容
完成 RedBlackTree.java 中的以下方法:
flipColorsrotateRight和rotateLeftinsert这个实验值 5 分。