作业 3 | CS 61A 2024 春季学期

作业 3：递归，树递归

hw03.zip

截止时间：2 月 15 日，星期四，晚上 11:59

操作指南

下载 hw03.zip。在压缩文件中，你会找到一个名为 hw03.py 的文件，以及 ok 自动评分器程序。

提交： 完成后，请将你编辑的所有代码文件上传到 Gradescope 以提交你的作业。你可以在截止时间前多次提交；只有最后一次提交会被评分。请确认你在 Gradescope 上成功提交了代码。有关提交作业的更多说明，请参阅 Lab 0。

使用 Ok： 如果你对使用 Ok 有任何疑问，请参阅这份指南。

阅读材料： 你可能会发现以下参考资料很有用：

第 1.7 节

评分： 家庭作业根据正确性评分。每个不正确的问题将使总分减少一分。此家庭作业满分为 2 分。

作业题目

入门指导视频

这些视频可能会为解决此作业中的编码问题提供一些有用的指导。

要观看这些视频，你需要登录你的 berkeley.edu 邮箱。

YouTube 链接

Q1：Num Eights

编写一个递归函数 num_eights，该函数接受一个正整数 n 并返回数字 8 在 n 中出现的次数。

注意： 使用递归；如果使用了赋值语句或者循环，测试将无法通过。（但是，可以使用函数定义来实现。）

def num_eights(n):
    """Returns the number of times 8 appears as a digit of n.

    >>> num_eights(3)
    0
    >>> num_eights(8)
    1
    >>> num_eights(88888888)
    8
    >>> num_eights(2638)
    1
    >>> num_eights(86380)
    2
    >>> num_eights(12345)
    0
    >>> num_eights(8782089)
    3
    >>> from construct_check import check
    >>> # ban all assignment statements
    >>> check(HW_SOURCE_FILE, 'num_eights',
    ...       ['Assign', 'AnnAssign', 'AugAssign', 'NamedExpr', 'For', 'While'])
    True
    """
    "*** YOUR CODE HERE ***"

用 Ok 运行你的代码：

python3 ok -q num_eights

Q2：Digit Distance

对于给定的整数，digit distance 指的是一个数中，相邻两位数字之差的绝对值的总和。例如：

6 的 digit distance 为 0。
61 的 digit distance 为 5，因为 6 - 1 的绝对值为 5。
71253 的 digit distance 为 12 (6 + 1 + 3 + 2)。

写一个函数来计算给定正整数的 digit distance。你必须使用递归，否则测试将失败。

提示： 有多种有效的方法可以解决这个问题！如果你遇到困难，可以先尝试编写一个迭代的解决方案，然后再将迭代的解决方案转换为递归的解决方案。

def digit_distance(n):
    """Determines the digit distance of n.

    >>> digit_distance(3)
    0
    >>> digit_distance(777)
    0
    >>> digit_distance(314)
    5
    >>> digit_distance(31415926535)
    32
    >>> digit_distance(3464660003)
    16
    >>> from construct_check import check
    >>> # ban all loops
    >>> check(HW_SOURCE_FILE, 'digit_distance',
    ...       ['For', 'While'])
    True
    """
    "*** YOUR CODE HERE ***"

用 Ok 测试你的代码：

python3 ok -q digit_distance

Q3: 交错求和

编写一个名为 interleaved_sum 的函数，该函数接受一个数字 n 以及两个单参数函数 odd_func 和 even_func。此函数将 odd_func 应用于 1 到 n（包括 n）之间的每个奇数，将 even_func 应用于每个偶数，并返回总和。

例如，执行 interleaved_sum(5, lambda x: x, lambda x: x * x) 返回 1 + 2*2 + 3 + 4*4 + 5 = 29。

实现此函数，无需使用任何循环或直接判断数字的奇偶性——不允许使用模数 (%)！应该从 1 开始，因为它是一个奇数。

提示：引入一个内部辅助函数，该函数接受一个奇数 k 并计算从 k 到 n（包括 n）的交错和。

def interleaved_sum(n, odd_func, even_func):
    """Compute the sum odd_func(1) + even_func(2) + odd_func(3) + ..., up
    to n.

    >>> identity = lambda x: x
    >>> square = lambda x: x * x
    >>> triple = lambda x: x * 3
    >>> interleaved_sum(5, identity, square) # 1   + 2*2 + 3   + 4*4 + 5
    29
    >>> interleaved_sum(5, square, identity) # 1*1 + 2   + 3*3 + 4   + 5*5
    41
    >>> interleaved_sum(4, triple, square)   # 1*3 + 2*2 + 3*3 + 4*4
    32
    >>> interleaved_sum(4, square, triple)   # 1*1 + 2*3 + 3*3 + 4*3
    28
    >>> from construct_check import check
    >>> check(HW_SOURCE_FILE, 'interleaved_sum', ['While', 'For', 'Mod']) # ban loops and %
    True
    """
    "*** YOUR CODE HERE ***"

用 Ok 测试你的代码：

python3 ok -q interleaved_sum

Q4: 数硬币

给定一个正整数 total，如果硬币值的总和为 total，则一组硬币可以兑换 total。在这里，我们将使用标准美国硬币值：1、5、10、25。例如，以下集合可以兑换 15：

15个1美分的硬币
10个1美分的硬币，1个5美分的硬币
5个1美分的硬币，2个5美分的硬币
5个1美分的硬币，1个10美分的硬币
3个5美分的硬币
1个5美分的硬币，1个10美分的硬币

因此，15 有 6 种兑换方式。编写一个递归函数 count_coins，它接受一个正整数 total 作为输入，并返回用硬币凑出总金额 total 的组合数。

你可以使用以下给定的函数：

next_larger_coin 函数会返回比输入面额更大的下一种硬币面额。例如，next_larger_coin(5) 的返回值是 10。
next_smaller_coin 函数会返回比输入面额更小的下一种硬币面额。例如，next_smaller_coin(5) 的返回值是 1。
如果不存在更大或更小的硬币面额，则任一函数将返回 None。

解决这个问题主要有两种思路：一种是使用 next_larger_coin 函数，另一种是使用 next_smaller_coin 函数。

重要：必须使用递归方法；使用循环会导致测试失败。

提示：可以参考 count_partitions 函数的实现，学习如何用较小的部分凑出目标总和。如果需要在递归调用中记录多个状态，可以考虑编写辅助函数。

def next_larger_coin(coin):
    """Returns the next larger coin in order.
    >>> next_larger_coin(1)
    5
    >>> next_larger_coin(5)
    10
    >>> next_larger_coin(10)
    25
    >>> next_larger_coin(2) # Other values return None
    """
    if coin == 1:
        return 5
    elif coin == 5:
        return 10
    elif coin == 10:
        return 25

def next_smaller_coin(coin):
    """Returns the next smaller coin in order.
    >>> next_smaller_coin(25)
    10
    >>> next_smaller_coin(10)
    5
    >>> next_smaller_coin(5)
    1
    >>> next_smaller_coin(2) # Other values return None
    """
    if coin == 25:
        return 10
    elif coin == 10:
        return 5
    elif coin == 5:
        return 1

def count_coins(total):
    """Return the number of ways to make change using coins of value of 1, 5, 10, 25.
    >>> count_coins(15)
    6
    >>> count_coins(10)
    4
    >>> count_coins(20)
    9
    >>> count_coins(100) # How many ways to make change for a dollar?
    242
    >>> count_coins(200)
    1463
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'count_coins', ['While', 'For'])
    True
    """
    "*** YOUR CODE HERE ***"

使用 Ok 运行测试：

python3 ok -q count_coins

在本地查看你的分数

你可以通过运行以下命令在本地查看你在本次作业中每个题目的得分

python3 ok --score

请注意，这不会提交你的作业！当你对得分满意后，请将作业提交到 Gradescope 以获得相应分数。

提交

请将你编辑过的所有文件上传到Gradescope上对应的作业以提交本次作业。Lab 00 提供了详细的提交说明。

此外，所有没有参加大型实验课的学生都需要填写考勤表。无论您是否参加了实验课，或者因为正当理由错过了实验课，请每周提交此表格。大型实验课的学生不需要填写考勤表。

考试练习

本次作业中还包含往年的考试题目，供大家参考。这些题目不计入成绩，仅供练习，欢迎大家尝试挑战！

2017年秋季MT1 Q4a: Digital
2018年夏季MT1 Q5a: Won't You Be My Neighbor?
2019年秋季Final Q6b: Palindromes

仅供娱乐的问题

以下问题难度超出61A课程范围。欢迎大家尝试这些附加挑战题，但它们并非课程要求。大部分同学可以选择跳过这些题目，不会影响课程成绩。我们不会优先解答关于这些题目的问题，请同学们理解。

Q5: 汉诺塔

一个经典的谜题叫做汉诺塔，它是一个由三根杆子和许多不同大小的圆盘组成的游戏，这些圆盘可以滑到任意一根杆子上。这个谜题开始时，n 个圆盘整齐地堆叠在一个 start 杆上，大小按升序排列，最小的在顶部，形成一个圆锥形。

汉诺塔

这个谜题的目标是将整个堆栈移动到 end 杆上，遵守以下规则：

一次只能移动一个圆盘。
每次移动包括从其中一根杆子上取下顶部（最小的）圆盘，然后将其滑到另一根杆子上，放在可能已经存在于该杆子上的其他圆盘的顶部。
任何圆盘都不能放在较小的圆盘之上。

完成 move_stack 的定义，它会打印出将 n 个圆盘从 start 杆移动到 end 杆所需的步骤，而不会违反规则。提供的 print_move 函数将打印出将单个圆盘从给定的 origin 移动到给定的 destination 的步骤。

提示： 在一张纸上画出几个具有不同 n 的游戏，并尝试找到适用于任何 n 的圆盘移动模式。在解答过程中，当需要将少于n个圆盘从一根杆子移动到另一根杆子时，可以大胆使用递归。如果您需要更多帮助，请参阅以下提示。

请参阅以下汉诺塔动画，该动画由用户 Trixx 在 Wikimedia 上找到。

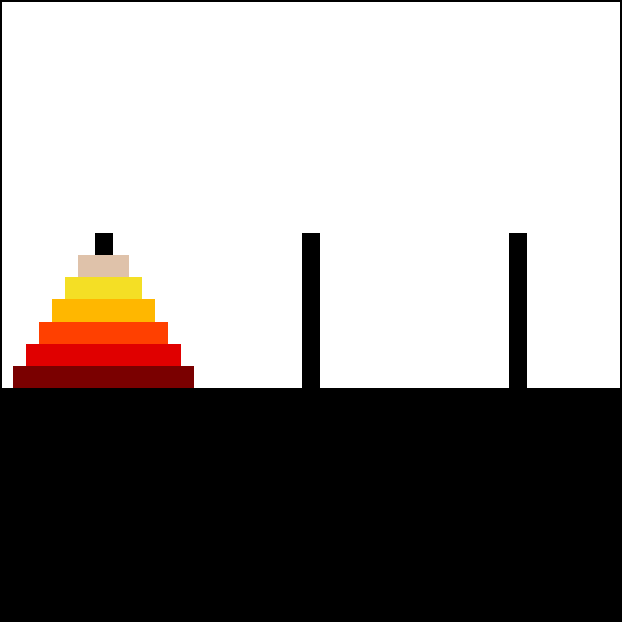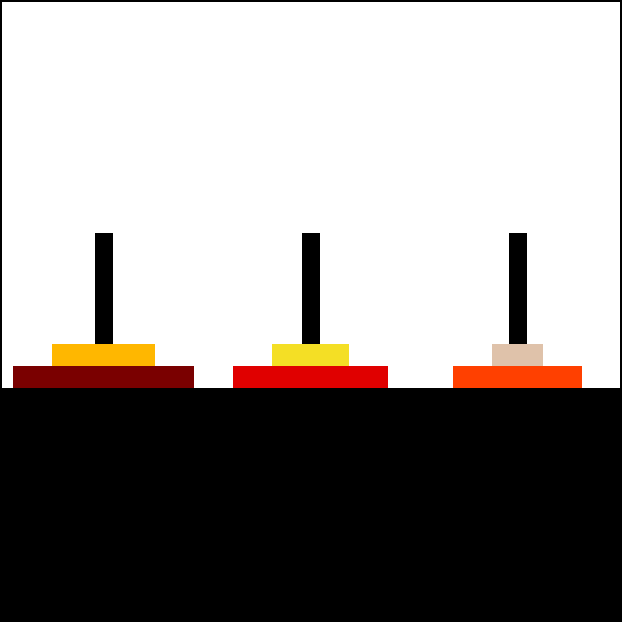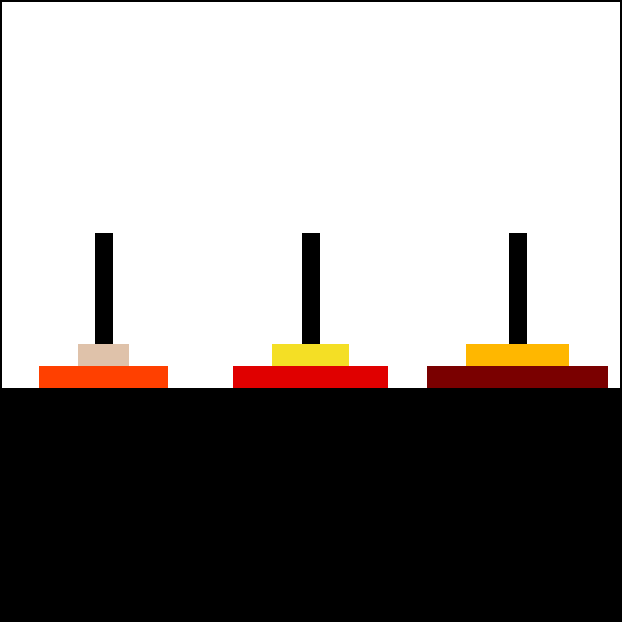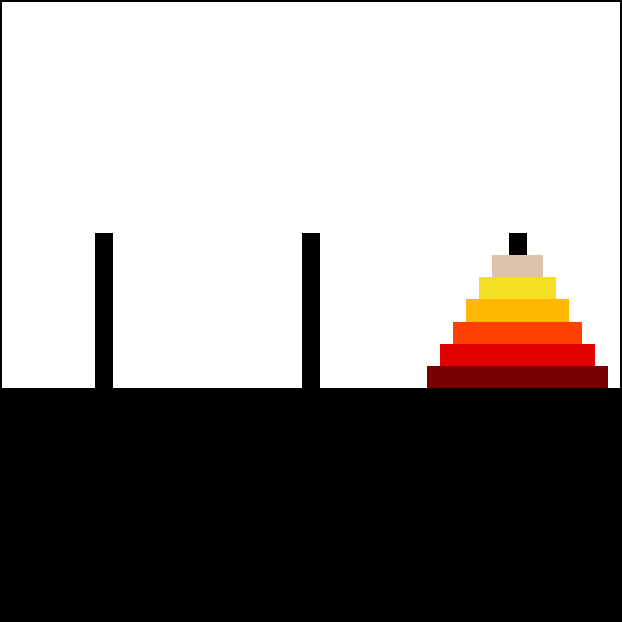汉诺塔的解题策略是先将除了最底部的圆盘之外的所有圆盘移动到辅助柱（通常是第二个柱子）上，然后将最底部的圆盘移动到目标柱（第三个柱子）上，最后将辅助柱上的所有圆盘移动到目标柱上。

你无需担心如何记录每一步的操作。print 实际上会在终端中“收集”所有结果，只要你确保按顺序打印移动步骤即可。

def print_move(origin, destination):
    """Print instructions to move a disk."""
    print("Move the top disk from rod", origin, "to rod", destination)

def move_stack(n, start, end):
    """Print the moves required to move n disks on the start pole to the end
    pole without violating the rules of Towers of Hanoi.

    n -- number of disks
    start -- a pole position, either 1, 2, or 3
    end -- a pole position, either 1, 2, or 3

    There are exactly three poles, and start and end must be different. Assume
    that the start pole has at least n disks of increasing size, and the end
    pole is either empty or has a top disk larger than the top n start disks.

    >>> move_stack(1, 1, 3)
    Move the top disk from rod 1 to rod 3
    >>> move_stack(2, 1, 3)
    Move the top disk from rod 1 to rod 2
    Move the top disk from rod 1 to rod 3
    Move the top disk from rod 2 to rod 3
    >>> move_stack(3, 1, 3)
    Move the top disk from rod 1 to rod 3
    Move the top disk from rod 1 to rod 2
    Move the top disk from rod 3 to rod 2
    Move the top disk from rod 1 to rod 3
    Move the top disk from rod 2 to rod 1
    Move the top disk from rod 2 to rod 3
    Move the top disk from rod 1 to rod 3
    """
    assert 1 <= start <= 3 and 1 <= end <= 3 and start != end, "Bad start/end"
    "*** YOUR CODE HERE ***"

Use Ok to test your code:

python3 ok -q move_stack

Q6: 无名函数实现的阶乘

这个问题展示了如何在不使用全局变量名定义递归函数的情况下，实现递归。

递归阶乘函数可以使用条件表达式编写为单个表达式。

>>> fact = lambda n: 1 if n == 1 else mul(n, fact(sub(n, 1)))
>>> fact(5)
120

但是，这个实现依赖于fact这个名称，我们在函数体中会引用它。要编写递归函数，我们总是使用 def 或赋值语句为其命名，以便我们可以在其自身的主体中引用该函数。在这个问题中，你的任务是在不给它命名的情况下递归地定义 fact！

编写一个表达式，仅使用调用表达式、条件表达式和 lambda 表达式（没有赋值或 def 语句）来计算 n 阶乘。

注意： 你不能在你的返回表达式中使用 make_anonymous_factorial。

operator 模块中的 sub 和 mul 函数是解决此问题所需的唯一内置函数。

from operator import sub, mul

def make_anonymous_factorial():
    """返回一个计算阶乘的表达式的值。

>>> make_anonymous_factorial()(5)
    120
    >>> from construct_check import check
    >>> # 禁止使用赋值语句和递归
    >>> check(HW_SOURCE_FILE, 'make_anonymous_factorial',
    ...     ['Assign', 'AnnAssign', 'AugAssign', 'NamedExpr', 'FunctionDef', 'Recursion'])
    True
    """
    return 'YOUR_EXPRESSION_HERE'

使用 Ok 来测试你的代码:

python3 ok -q make_anonymous_factorial

作业 3 | CS 61A 2024 春季学期

作业 3：递归，树递归​

操作指南​

作业题目​

入门指导视频​

Q1：Num Eights​

Q2：Digit Distance​

Q3: 交错求和​

Q4: 数硬币​

在本地查看你的分数​

提交​

考试练习​

仅供娱乐的问题​

Q5: 汉诺塔​

Q6: 无名函数实现的阶乘​