家庭作业 4 答案 | CS 61A 2024 年春季
家庭作业 4 答案
答案文件
你可以在 hw04.py 找到答案。
必做题目
新手视频
这些视频可以帮助你解决作业中的编程问题。
要观看这些视频，你应该登录你的 berkeley.edu 电子邮件。
序列
Q1: 深度映射 (Deep Map)
请编写一个函数 deep_map，它接受一个列表 s 和一个单参数函数 f。s 可以是嵌套列表，也就是列表中包含列表。deep_map 会修改 s，将 s 或其包含的任何列表中的每个元素替换为调用 f 的结果。
deep_map 返回 None 并且不应创建任何新列表。
提示： 如果
a是一个列表，type(a) == list将评估为True。
def deep_map(f, s):
"""Replace all non-list elements x with f(x) in the nested list s.
>>> six = [1, 2, [3, [4], 5], 6]
>>> deep_map(lambda x: x * x, six)
>>> six
[1, 4, [9, [16], 25], 36]
>>> # Check that you're not making new lists
>>> s = [3, [1, [4, [1]]]]
>>> s1 = s[1]
>>> s2 = s1[1]
>>> s3 = s2[1]
>>> deep_map(lambda x: x + 1, s)
>>> s
[4, [2, [5, [2]]]]
>>> s1 is s[1]
True
>>> s2 is s1[1]
True
>>> s3 is s2[1]
True
"""
for i in range(len(s)):
if type(s[i]) == list:
deep_map(f, s[i])
else:
s[i] = f(s[i])
使用 Ok 测试你的代码:
python3 ok -q deep_map
数据抽象
鸣谢
这个问题基于计算机程序的构造和解释 第 2.2.2 节。
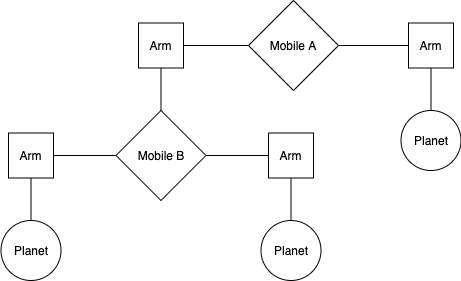我们要做一个天文馆主题的悬挂模型。这种悬挂模型是一种悬挂式雕塑。一个二元悬挂模型由两根悬臂组成。每根悬臂都是有一定长度的杆子，杆子上悬挂着一个行星或者另一个悬挂模型。例如，下图展示了悬挂模型 A 的左悬臂和右悬臂，以及每根悬臂末端悬挂的物体。
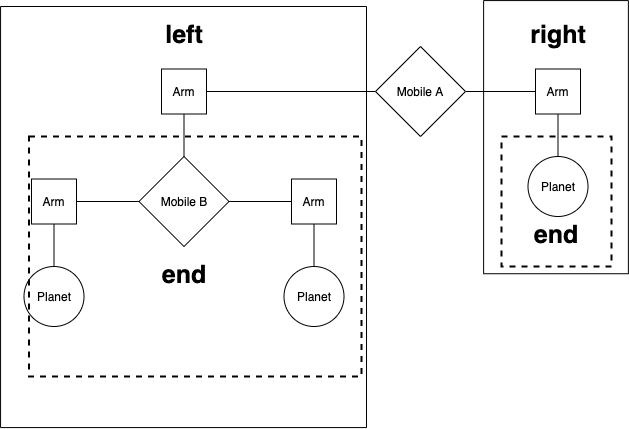
我们将使用以下数据抽象来表示二元悬挂模型。
- 一个
mobile必须包含一个左arm和一个右arm。 - 一个
arm必须有正的长度，并且末端悬挂着一个mobile或者一个planet。 - 一个
planet具有正质量，并且没有任何东西悬挂在它上面。
下面是用于悬挂模型中各种数据抽象的实现。mobile 和 arm 数据抽象已为您完成。
悬挂模型数据抽象的实现 (供您参考，无需在此处执行任何操作)：
def mobile(left, right):
"""Construct a mobile from a left arm and a right arm."""
assert is_arm(left), "left must be an arm"
assert is_arm(right), "right must be an arm"
return ['mobile', left, right]
def is_mobile(m):
"""Return whether m is a mobile."""
return type(m) == list and len(m) == 3 and m[0] == 'mobile'
def left(m):
"""Select the left arm of a mobile."""
assert is_mobile(m), "must call left on a mobile"
return m[1]
def right(m):
"""Select the right arm of a mobile."""
assert is_mobile(m), "must call right on a mobile"
return m[2]
Arm 数据抽象的实现 (供您参考，无需在此处执行任何操作)：
def arm(length, mobile_or_planet):
"""Construct an arm: a length of rod with a mobile or planet at the end."""
assert is_mobile(mobile_or_planet) or is_planet(mobile_or_planet)
return ['arm', length, mobile_or_planet]
def is_arm(s):
"""Return whether s is an arm."""
return type(s) == list and len(s) == 3 and s[0] == 'arm'
def length(s):
"""Select the length of an arm."""
assert is_arm(s), "must call length on an arm"
return s[1]
def end(s):
"""Select the mobile or planet hanging at the end of an arm."""
assert is_arm(s), "must call end on an arm"
return s[2]
Q2: 质量（Mass）
通过完成 planet 构造函数和 mass 选择器来实现 planet 数据抽象，以便使用一个包含两个元素的列表来表示行星，其中第一个元素是字符串 'planet'，第二个元素是它的质量。
def planet(mass):
"""构造一个具有一定质量的行星。"""
assert mass > 0
return ['planet', mass]
def mass(p):
"""选择一个行星的质量。"""
assert is_planet(p), '必须对行星调用 mass 函数'
return p[1]
def is_planet(p):
"""判断 p 是否为行星。"""
return type(p) == list and len(p) == 2 and p[0] == 'planet'
total_mass 函数演示了 mobile、arm 和 planet 数据抽象的用法。你无需在此处编写任何代码。在后续问题中，你可以使用 total_mass 函数。
def examples():
t = mobile(arm(1, planet(2)),
arm(2, planet(1)))
u = mobile(arm(5, planet(1)),
arm(1, mobile(arm(2, planet(3)),
arm(3, planet(2)))))
v = mobile(arm(4, t), arm(2, u))
return t, u, v
def total_mass(m):
"""返回 m 的总质量，m 可以是行星或 mobile。
>>> t, u, v = examples()
>>> total_mass(t)
3
>>> total_mass(u)
6
>>> total_mass(v)
9
"""
if is_planet(m):
return mass(m)
else:
assert is_mobile(m), "必须获取 mobile 或行星的总质量"
return total_mass(end(left(m))) + total_mass(end(right(m)))
运行 ok 测试 total_mass，确保 planet 和 mass 函数的实现正确。
使用 Ok 测试你的代码：
python3 ok -q total_mass
Q3: Balanced
实现 balanced 函数，判断 m 是否为平衡的 mobile。平衡的 mobile 需满足以下两个条件：
- 左臂产生的扭矩等于右臂产生的扭矩。左臂的扭矩等于左杆的长度乘以其悬挂的总质量。右臂亦然。例如，如果左臂的长度为
5，并且在左臂末端悬挂着一个总质量为10的mobile，则 mobile 左侧的扭矩为50。 - 每个悬挂在其臂末端的 mobile 自身也必须是平衡的。
行星本身是平衡的，因为没有任何东西悬挂在它们上面。
提示： 你可以使用上面的
total_mass函数。不要违反抽象屏障。而是使用已定义的选择器函数。
def balanced(m):
"""返回 m 是否平衡。
>>> t, u, v = examples()
>>> balanced(t)
True
>>> balanced(v)
True
>>> p = mobile(arm(3, t), arm(2, u))
>>> balanced(p)
False
>>> balanced(mobile(arm(1, v), arm(1, p)))
False
>>> balanced(mobile(arm(1, p), arm(1, v)))
False
>>> from construct_check import check
>>> # checking for abstraction barrier violations by banning indexing
>>> check(HW_SOURCE_FILE, 'balanced', ['Index'])
True
"""
如果 m 是一个行星:
返回 True
否则，
left_end, right_end = end(left(m)), end(right(m))
torque_left = length(left(m)) * total_mass(left_end)
torque_right = length(right(m)) * total_mass(right_end)
return torque_left == torque_right and balanced(left_end) and balanced(right_end)
使用 Ok 来测试你的代码:
python3 ok -q balanced
行星是平衡状态的这一事实很重要，因为我们将像许多其他树问题一样递归地解决这个问题（即使这并非显式地是一棵树）。
基本情况: 如果我们正在检查一个行星，那么我们知道它是平衡状态的。为什么这是一个合适的基本情况? 对此有两种可能的方法:
- 因为我们知道到目前为止我们的数据结构是树，行星是最简单的树，因为我们选择将它们实现为叶子。
- 我们也知道，从数据抽象的角度来看，行星是移动装置中的终端项目。因此，以此作为检查的终点是合理的。
否则: 请注意，重要的是进行递归调用以检查两个臂是否平衡。但是，我们还需要进行基本比较，即查看两个臂的总质量以及它们的长度。例如，如果两个臂都是一个行星，那么它们都将是平衡状态的。但是，只有当扭矩相等时，整个悬挂装置才能达到平衡；仅仅检查每个臂是否平衡是不充分的。
树
Q4：最大路径之和
编写一个函数，接收一棵树作为输入，返回从根到叶的任意路径上的最大值之和。根到叶路径是从根开始并进行到树的某个叶子的节点序列。您可以假设树的标签为正数。
def max_path_sum(t):
"""返回树的最大根到叶路径和。
>>> t = tree(1, [tree(5, [tree(1), tree(3)]), tree(10)])
>>> max_path_sum(t) # 1, 10
11
>>> t2 = tree(5, [tree(4, [tree(1), tree(3)]), tree(2, [tree(10), tree(3)])])
>>> max_path_sum(t2) # 5, 2, 10
17
"""
# 非列表推导式解决方案
if is_leaf(t):
return label(t)
highest_sum = 0
for b in branches(t):
highest_sum = max(max_path_sum(b), highest_sum)
return label(t) + highest_sum
```# 列表解析解法
if is_leaf(t):
return label(t)
else:
return label(t) + max([max_path_sum(b) for b in branches(t)])
使用 Ok 测试你的代码:
python3 ok -q max_path_sum
在本地查看你的得分
你可以通过运行以下命令在本地查看你在本次作业中每个题目的得分
python3 ok --score
这并不会提交作业！ 当你对你的分数感到满意时，请将你编辑过的文件上传到 Gradescope 上对应的作业中来提交本次作业。Lab 00 包含详细的说明。
考试练习
本次作业也包含了一些往年考试真题，供你参考。 这些题目不计入成绩，如果你想挑战一下自己，欢迎尝试！