CS 61A 2024 春季学期 | 家庭作业 4

家庭作业 4：序列、ADT 树

• hw04.zip

截止日期：2 月 29 日周四晚 11:59

须知

下载 hw04.zip。压缩包内含 [hw04.py] 文件以及 ok 自动评分器。

提交： 完成作业后，请将所有已编辑的代码文件上传至 Gradescope。截止日期前可多次提交，最终提交版本将被评分。请务必检查在 Gradescope 上是否成功提交。更多提交说明请参考 Lab 0。

使用 Ok： 如有关于 Ok 使用的问题，请参考本指南。

阅读材料： 以下参考资料可能对您有所帮助：

• 第 2.2 节
• 第 2.3 节
• 第 2.4 节

评分标准： 作业根据正确性评分，每错一题扣一分。本次作业总分 2 分。

必做题

入门视频

入门视频：这些视频将帮助你解决本次作业中的编程问题。

观看视频需登录 berkeley.edu 邮箱。

YouTube 链接

序列

Q1：深度映射

编写一个函数 deep_map，它接受一个列表 s 和一个单参数函数 f。s 可能是一个嵌套列表，即包含其他列表的列表。deep_map 通过将 s 或其包含的任何列表中的每个元素替换为对该元素调用 f 的结果来修改 s。

deep_map 返回 None 并且不应创建任何新列表。

提示： type(a) == list 在 a 为列表时返回 True。

def deep_map(f, s):
    """Replace all non-list elements x with f(x) in the nested list s.

    >>> six = [1, 2, [3, [4], 5], 6]
    >>> deep_map(lambda x: x * x, six)
    >>> six
    [1, 4, [9, [16], 25], 36]
    >>> # Check that you're not making new lists
    >>> s = [3, [1, [4, [1]]]]
    >>> s1 = s[1]
    >>> s2 = s1[1]
    >>> s3 = s2[1]
    >>> deep_map(lambda x: x + 1, s)
    >>> s
    [4, [2, [5, [2]]]]
    >>> s1 is s[1]
    True
    >>> s2 is s1[1]
    True
    >>> s3 is s2[1]
    True
    """
    "*** YOUR CODE HERE ***"

使用 Ok 测试您的代码：

python3 ok -q deep_map

数据抽象

鸣谢

此问题基于计算机程序的构造与解释 第 2.2.2 节 中的一个问题。

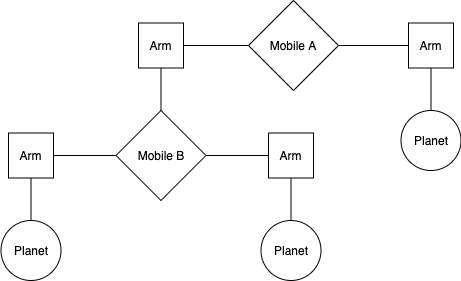
我们正在制作一个天文馆吊饰。一个 吊饰 是一种悬挂式雕塑。一个二元吊饰由两个臂组成。每个臂是一定长度的杆，杆上悬挂着一颗行星或另一个吊饰。例如，下图显示了吊饰 A 的左臂和右臂，以及悬挂在每个臂末端的物体。

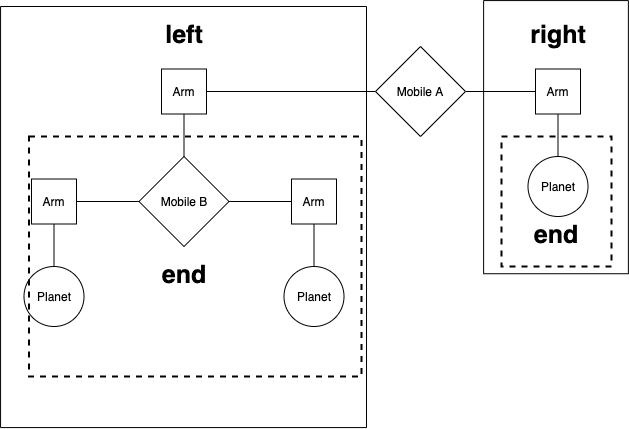
我们将使用以下数据抽象来表示二元吊饰。

• 一个 mobile 必须同时具有左 arm 和右 arm。
• 一个 arm 具有正长度，并且必须在末端悬挂一些东西，即 mobile 或 planet。
• 一个 planet 具有正质量，并且没有任何东西悬挂在它上面。

以下是用于吊饰的各种数据抽象的实现。mobile 和 arm 数据抽象已为您完成。

Mobile 数据抽象实现（仅供参考，无需修改）：

def mobile(left, right):
    """Construct a mobile from a left arm and a right arm."""
    assert is_arm(left), "left must be an arm"
    assert is_arm(right), "right must be an arm"
    return ['mobile', left, right]

def is_mobile(m):
    """Return whether m is a mobile."""
    return type(m) == list and len(m) == 3 and m[0] == 'mobile'

def left(m):
    """Select the left arm of a mobile."""
    assert is_mobile(m), "must call left on a mobile"
    return m[1]

def right(m):
    """Select the right arm of a mobile."""
    assert is_mobile(m), "must call right on a mobile"
    return m[2]

臂膀数据抽象的实现 (（仅供参考，无需修改）):

def arm(length, mobile_or_planet):
    """Construct an arm: a length of rod with a mobile or planet at the end."""
    assert is_mobile(mobile_or_planet) or is_planet(mobile_or_planet)
    return ['arm', length, mobile_or_planet]

def is_arm(s):
    """Return whether s is an arm."""
    return type(s) == list and len(s) == 3 and s[0] == 'arm'

def length(s):
    """Select the length of an arm."""
    assert is_arm(s), "must call length on an arm"
    return s[1]

def end(s):
    """Select the mobile or planet hanging at the end of an arm."""
    assert is_arm(s), "must call end on an arm"
    return s[2]

Q2: 质量 (Mass)

实现 planet 数据抽象，需要完成 planet 构造函数和 mass 选择器。 行星将用一个包含两个元素的列表表示：第一个元素是字符串 'planet'，第二个元素是它的质量。

def planet(mass):
    """Construct a planet of some mass."""
    assert mass > 0
    "*** YOUR CODE HERE ***"

def mass(p):
    """Select the mass of a planet."""
    assert is_planet(p), 'must call mass on a planet'
    "*** YOUR CODE HERE ***"

def is_planet(p):
    """Whether p is a planet."""
    return type(p) == list and len(p) == 2 and p[0] == 'planet'

total_mass 函数演示了 mobile、arm 和 planet 抽象的用法。 你不需要在这里实现任何东西。你可以在以下问题中使用 total_mass 函数。

def examples():
    t = mobile(arm(1, planet(2)),
               arm(2, planet(1)))
    u = mobile(arm(5, planet(1)),
               arm(1, mobile(arm(2, planet(3)),
                             arm(3, planet(2)))))
    v = mobile(arm(4, t), arm(2, u))
    return t, u, v

def total_mass(m):
    """Return the total mass of m, a planet or mobile.

    >>> t, u, v = examples()
    >>> total_mass(t)
    3
    >>> total_mass(u)
    6
    >>> total_mass(v)
    9
    """
    if is_planet(m):
        return mass(m)
    else:
        assert is_mobile(m), "must get total mass of a mobile or a planet"
        return total_mass(end(left(m))) + total_mass(end(right(m)))

运行 ok 测试 total_mass，确保 planet 和 mass 函数已正确实现。

用 Ok 测试你的代码:

python3 ok -q total_mass

Q3: 平衡

实现 balanced 函数，判断 m 是否为平衡的 mobile。 平衡需要满足以下两个条件：

1. 左臂和右臂的扭矩相等。 扭矩的计算方式是：杆的长度乘以悬挂在其上的总质量。 例如，左臂长为 5，悬挂的总质量为 10 的 mobile，则左侧扭矩为 50。
2. 每个手臂末端悬挂的 mobile 本身也必须是平衡的。

行星本身即为平衡。

你可以使用上面的 total_mass 函数。 不要违反抽象屏障，请使用已定义的选择器函数。

def balanced(m):
    """Return whether m is balanced.

    >>> t, u, v = examples()
    >>> balanced(t)
    True
    >>> balanced(v)
    True
    >>> p = mobile(arm(3, t), arm(2, u))
    >>> balanced(p)
    False
    >>> balanced(mobile(arm(1, v), arm(1, p)))
    False
    >>> balanced(mobile(arm(1, p), arm(1, v)))
    False
    >>> from construct_check import check
    >>> # checking for abstraction barrier violations by banning indexing
    >>> check(HW_SOURCE_FILE, 'balanced', ['Index'])
    True
    """
    "*** YOUR CODE HERE ***"

使用 Ok 测试你的代码:

python3 ok -q balanced

树

Q4: 最大路径和

编写一个函数，输入一棵树，返回从根节点到叶节点的所有路径中，节点值之和的最大值。 假设树的所有节点值均为正数。

def max_path_sum(t):
    """返回这棵树从根节点到叶节点的最大路径和。
    >>> t = tree(1, [tree(5, [tree(1), tree(3)]), tree(10)])
    >>> max_path_sum(t) # 1, 10
    11
    >>> t2 = tree(5, [tree(4, [tree(1), tree(3)]), tree(2, [tree(10), tree(3)])])
    >>> max_path_sum(t2) # 5, 2, 10
    17
    """
    "*** YOUR CODE HERE ***"

用 Ok 测试你的代码：

python3 ok -q max_path_sum