CS 61A 2024春季学期作业7答案
Homework 7 答案
解答文件
您可以在 hw07.scm 中找到解答。
每个Scheme作业都自带61A Scheme解释器。要启动它,请打开终端并输入 python3 scheme。要加载名为 f.scm 的 Scheme 文件,请键入 python3 scheme -i f.scm。要退出 Scheme 解释器,请键入 (exit)。
Scheme 编辑器
所有Scheme作业都提供一个网页编辑器,方便运行ok测试和可视化环境。在终端输入python3 editor,编辑器会在浏览器中打开,地址是http://127.0.0.1:31415/。要停止编辑器并返回命令行,请在启动编辑器的终端窗口中按Ctrl-C。
“运行”按钮会加载当前作业的.scm文件,并启动Scheme解释器,方便你尝试运行不同的Scheme表达式。
“测试”按钮会运行所有针对本次作业的ok测试。如果测试失败,可以点击“查看案例”,然后点击“调试”来单步调试。
推荐使用的 VS Code 扩展
如果您选择使用 VS Code 作为文本编辑器(而不是网页编辑器),请安装 vscode-scheme 扩展,以便突出显示括号。
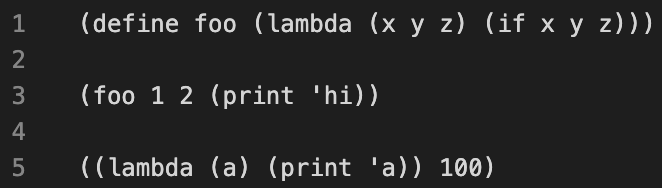
之前:
之后:
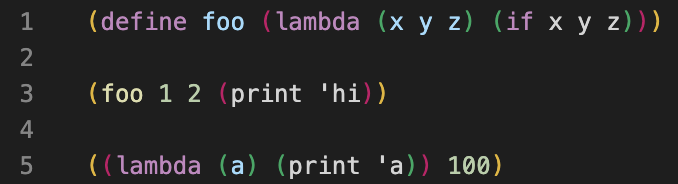
此外,还有一个名为61a-bot的VS Code扩展(安装说明),可以用于Scheme作业。这个bot也集成到了ok中。
作业必做题
新手入门视频
这些视频可能会为解决此作业中的编码问题提供一些有用的指导。
要观看这些视频,请使用您的berkeley.edu邮箱账号登录。
Q1: Pow
实现一个名为pow的函数,计算base的exp次幂,其中exp为非负整数。递归调用pow的次数应该以对数级别增长,而不是线性级别(与exp的大小相比)。例如,调用(pow 2 32)应该只需要5次递归调用,而不是32次。
提示:
- x2y = (xy)2
- x2y+1 = x(xy)2
例如,216 = (28)2 和 217 = 2 * (28)2。
你可以使用内置的
even?和odd?函数。此外,我们已经为你定义好了square函数。Scheme语言没有
while和for循环,所以你需要使用递归来解决这个问题。
(define (square n) (* n n))
(define (pow base exp)
(cond ((= exp 0) 1)
((even? exp) (square (pow base (/ exp 2))))
(else (* base (pow base (- exp 1))))))
使用 Ok 测试您的代码:
python3 ok -q pow
当exp是偶数时,我们通过计算base^(exp/2)的平方来避免不必要的pow调用。
else分支处理exp为奇数的情况,将base^(exp-1)的结果乘以base。
当exp是偶数时,计算base^exp所需的调用次数比计算base^(exp/2)多一次。当exp是奇数时,计算base^exp所需的调用次数比计算base^((exp-1)/2)多两次。
因此,pow函数的时间复杂度是关于exp的对数级别。
Q2: Repeatedly Cube
实现一个名为repeatedly-cube的函数,该函数接收一个数字x,并对其进行n次立方操作。
以下是一些repeatedly-cube函数的示例:
scm> (repeatedly-cube 100 1) ; 1 立方 100 次结果仍然是 1
1
scm> (repeatedly-cube 2 2) ; (2^3)^3
512
scm> (repeatedly-cube 3 2) ; ((2^3)^3)^3
134217728
关于
let的更多信息,请参考 Scheme 规范。
(define (repeatedly-cube n x)
(if (zero? n)
x
(let
((y (repeatedly-cube (- n 1) x))) (* y y y))))
使用 Ok 来测试你的代码:
python3 ok -q repeatedly-cube
我们知道这个解法必须使用递归,因为 Scheme 在处理递归问题上比迭代更有优势。
当 n 为零时,提供的代码会返回 x。 这是 repeatedly-cube 的正确基本情况; 接下来,我们需要编写递归情况。
在递归的情况中,提供的代码返回 (* y y y),也就是 y 的立方。 我们通过递归调用,将 y 赋值为 x 立方 n - 1 次的结果。 这样,y 的立方就相当于将 x 立方 n 次,符合预期。
Q3: Cadr
提示: 关于 Scheme 列表的内容,请参考 4 月 3 日星期三的讲座视频。
定义过程 cadr,它返回列表的第二个元素。 另请定义 caddr,它返回列表的第三个元素。
(define (cddr s)
(cdr (cdr s)))
(define (cadr s)
(car (cdr s)))
(define (caddr s)
(car (cddr s)))
列表 s 的第二个元素,实际上就是 s 的 cdr 的第一个元素。 因此,(cadr s) 可以定义为 (car (cdr s))。
提供的 cddr 过程接收一个列表 s,并返回一个以 s 的第三个元素开始的新列表。 因此,(caddr s) 可以定义为 (car (cddr s))。
使用 Ok 测试你的代码:
python3 ok -q cadr-caddr