讨论 4 | CS 61A 2024 春季学期

讨论 4：树递归

• disc04.pdf

小组选一个人加入 Discord。多人加入也行，但一个人就够了。

现在切换到 Pensieve：

• 所有人：前往 discuss.pensieve.co 并使用您的 @berkeley.edu 邮箱登录，然后输入您的组号。（您的组号是您的 Discord 频道号。）

进入 Pensieve 后，您无需返回此页面；Pensieve 具有所有相同的内容（但功能更多）。 如果由于某种原因 Pensieve 无法工作，请返回此页面并继续讨论。

如果您遇到问题，请在 Discord 上的 #help 频道中发帖。

开始

为了呼应今天树递归的主题，请大家介绍一下自己的名字，以及最喜欢的一棵树（可以是具体的树，也可以是树的种类）。 树递归函数是指会多次调用自身的函数。

在本次讨论中，在您确信您的解决方案正确之前，请勿使用 Python 解释器来运行代码。 通过思考代码的运行结果来解决问题并检查代码。 不确定？ 与您的小组讨论！

[新内容] 如果小组人数不足 4 人，可以和同房间的其他小组合并。

[新内容] 递归需要练习。 如果您正在努力编写递归函数，请不要气馁。 相反，每次解决问题后（即使是在帮助下或小组合作完成），都请记录下为了取得进展，你意识到了什么。 学生通过实践和反思来提高。

[为了好玩] 这个戴牛仔帽的家伙的表情符号是有效的 Python：o[:-D]

>>> o = [2, 0, 2, 4]
>>> [ o[:-D] for D in range(1,4) ]
[[2, 0, 2], [2, 0], [2]]

🤠

树递归

对于以下问题，不要立即开始尝试编写代码。 而是首先用文字描述递归情况。 一些例子：

• 在讲座中的 fib 中，递归情况是将前两个斐波那契数加在一起。
• 在实验中的 double_eights 中，递归情况是检查数字的其余部分中是否有双 8。
• 在讲座中提到的 count_partitions 函数里，递归的情况是：使用最大为 m 的数来划分 n-m，并且使用最大为 m-1 的数来划分 n。

Q1：昆虫组合学

一只昆虫在一个 m x n 的网格里。 昆虫从左下角 (1, 1) 开始，想要到达右上角 (m, n)。 昆虫只能向上或向右移动。 编写一个 paths 函数，输入网格的高度和宽度，返回昆虫从起点到终点的路径总数。这个问题存在闭式解，但请尝试用递归方法来解决。

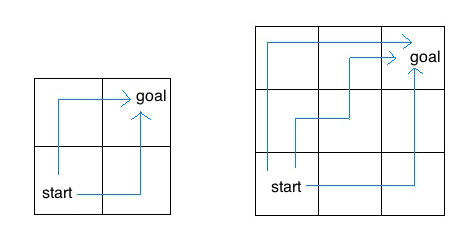
在 2 x 2 的网格中，昆虫有两条从起点到终点的路径。 在 3 x 3 的网格中，昆虫有六条路径（上面只显示了三条）。

提示： 如果昆虫到达网格的上边界或右边界会怎样？

def paths(m, n):
    """Return the number of paths from one corner of an
    M by N grid to the opposite corner.

    >>> paths(2, 2)
    2
    >>> paths(5, 7)
    210
    >>> paths(117, 1)
    1
    >>> paths(1, 157)
    1
    """
    "*** YOUR CODE HERE ***"

在 61A 代码平台运行 讲解环节： 小组达成一致方案后，就该练习如何清晰地解释递归逻辑了。选出一位展示者，然后在 discuss-queue 频道发送带有 @discuss 标签的消息，内容包括小组编号和 "Here's the path!"。助教会加入语音频道，听取讲解并给出反馈。

列表的树递归

【新】 有些同学可能已经了解了我们还没讲到的列表操作，比如 append。今天请先不要使用。只需要使用列表字面量 (例如 [1, 2, 3])、元素选择 (例如 s[0])、列表相加 (例如 [1] + [2, 3])、len 函数 (例如 len(s)) 和切片 (例如 s[1:])。下周我们介绍其他列表操作时，会有充足的时间。

关于列表，最重要的是要记住，任何非空列表 s 都可以拆分成第一个元素 s[0] 和剩余部分 s[1:]。

>>> s = [2, 3, 6, 4]
>>> s[0]
2
>>> s[1:]
[3, 6, 4]

Q2: 最大乘积

实现 max_product，它接受一个数字列表，并返回可以通过将列表中非连续元素相乘形成的最大乘积。假设输入列表中的所有数字都大于或等于 1。

def max_product(s):
    """Return the maximum product of non-consecutive elements of s.

    >>> max_product([10, 3, 1, 9, 2])   # 10 * 9
    90
    >>> max_product([5, 10, 5, 10, 5])  # 5 * 5 * 5
    125
    >>> max_product([])                 # The product of no numbers is 1
    1
    """

在 61A 代码平台运行

[提示]

首先尝试将第一个元素乘以剩余元素的 max_product (跳过与第一个元素相邻的第二个元素)，然后尝试跳过第一个元素，计算剩余元素的 max_product。使用 max 函数来比较这两种结果，取较大值。

遇到问题时，欢迎与助教交流！

请小组合作完成这句话，并将答案发送到小组的[频道文本聊天]中。“递归情况是选择 ... 和 ... 中较大的一个”

Q3: 求和问题

实现 sums(n, m)，它接受总数 n 和最大值 m。它返回所有列表的列表：

1. 总和为 n，
2. 仅包含高达 m 的正数，并且
3. 其中没有两个相邻的数字相同。

数字相同但顺序不同的列表都要返回。

以下是一个递归方法，与模板相符：对于从 1 到 m 的每个 k，构建所有总和为 n 且以 k 开头的列表，并将它们添加到 result 列表中。

提示： 使用 [k] + s (其中 k 是一个数字，s 是一个列表) 来构建一个以 k 开头的新列表。

>>> k = 2
>>> s = [4, 3, 1]
>>> [k] + s
[2, 4, 3, 1]

def sums(n, m):
    """Return lists that sum to n containing positive numbers up to m that
    have no adjacent repeats.

    >>> sums(5, 1)
    []
    >>> sums(5, 2)
    [[2, 1, 2]]
    >>> sums(5, 3)
    [[1, 3, 1], [2, 1, 2], [2, 3], [3, 2]]
    >>> sums(5, 5)
    [[1, 3, 1], [1, 4], [2, 1, 2], [2, 3], [3, 2], [4, 1], [5]]
    >>> sums(6, 3)
    [[1, 2, 1, 2], [1, 2, 3], [1, 3, 2], [2, 1, 2, 1], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]]
    """
    if n < 0:
        return []
    if n == 0:
        sums_to_zero = []     # The only way to sum to zero using positives
        return [sums_to_zero] # Return a list of all the ways to sum to zero
    result = []
    for k in range(1, m + 1):
        result = result + [ ___ for rest in ___ if rest == [] or ___ ]
    return result

Run in 61A Code

[提示信息]

k 是列表中加起来总和为 n 的列表的第一个数字，rest 则是列表剩余的部分。因此，我们需要构建一个总和为 n 的列表。

调用 sums 函数来生成所有总和为 n-k 的列表。通过在这些列表的前面添加 k，就可以构建出总和为 n 的列表。

这里需要确保“没有两个相邻的数字是相同的”。因为 k 是你构建的列表的第一个数字，所以它不能和 rest 的第一个元素相同（也就是列表的第二个数字）。

如果您遇到困难并想与工作人员交谈，请在 Discord 上发帖！

记录本次活动

请大家填写出勤表（每人每周提交一次）。