Discussion 8 | CS 61A 2024 春季学期

Discussion 8: 链表，效率

disc08.pdf

最新： 从现在开始，我们将继续使用 Pensieve，但我们已经从 Pensieve 中移除了语音聊天功能。请使用 Discord 和课程人员语音交流。它更可靠，并且包含屏幕共享功能。随时在 Discord 的 #discuss-queue 频道中向 @discuss 发送消息，课程工作人员会加入您的语音频道。

请您小组中的某个人加入 Discord。可以多人加入，但一个人就够了。

现在切换到 Pensieve：

所有人：前往 discuss.pensieve.co 并使用您的 @berkeley.edu 邮箱登录，然后输入您的组号。（您的组号是您的 Discord 频道号。）

进入 Pensieve 后就不用回到这个页面了，Pensieve 上有同样的内容（而且功能更多）。如果由于某种原因 Pensieve 无法工作，请返回此页面并继续讨论。

如果遇到问题，可以在 Discord 的 #help 频道里提问/求助。

开始

如果您的团队只有 1 或 2 个人，您可以加入房间里的另一个团队。

每个人都说出你的名字和你的生日，然后告诉小组你参加过的最喜欢的生日派对（无论是你自己的生日还是别人的生日）。

专家提示： 小组通常要卡很久才会求助。尝试早点寻求帮助。我们非常乐于助人！您可能会学到一些东西。

链表

链表是一个 Link 对象或 Link.empty。

你可以用两种方法修改 Link 对象 s：

使用 s.first = ... 更改第一个元素
使用 s.rest = ... 更改其余元素

您可以通过调用 Link 创建一个新的 Link 对象：

Link(4) 创建一个长度为 1 且包含 4 的链表。
Link(4, s) 创建一个以 4 开头，后跟链表 s 的元素的链表。

class Link:
    """A linked list is either a Link object or Link.empty

    >>> s = Link(3, Link(4, Link(5)))
    >>> s.rest
    Link(4, Link(5))
    >>> s.rest.rest.rest is Link.empty
    True
    >>> s.rest.first * 2
    8
    >>> print(s)
    <3 4 5>
    """
    empty = ()

    def __init__(self, first, rest=empty):
        assert rest is Link.empty or isinstance(rest, Link)
        self.first = first
        self.rest = rest

    def __repr__(self):
        if self.rest:
            rest_repr = ', ' + repr(self.rest)
        else:
            rest_repr = ''
        return 'Link(' + repr(self.first) + rest_repr + ')'

    def __str__(self):
        string = '<'
        while self.rest is not Link.empty:
            string += str(self.first) + ' '
            self = self.rest
        return string + str(self.first) + '>'

主持人： 选择一种小组画图的方式。纸、白板或平板电脑都可以。如果您没有任何类似的东西，请询问房间里的另一个小组是否有额外的纸。

Q1：奇怪的循环

在实验中，有一个带有循环的 Link 对象，它表示一个无限重复的 1 列表。

>>> ones = Link(1)
>>> ones.rest = ones
>>> [ones.first, ones.rest.first, ones.rest.rest.first, ones.rest.rest.rest.first]
[1, 1, 1, 1]
>>> ones.rest is ones
True

实现 strange_loop，它不接受任何参数并返回一个 Link 对象 s，对于该对象，s.rest.first.rest 是 s。

绘制您要创建的链表的图片，然后编写代码来创建它。

主持人： 当大家看得差不多了，就可以说：“这玩意儿长啥样？”

要让 s.rest.first.rest 存在，s 的第二个元素（也就是 s.rest.first）必须也是个链表。

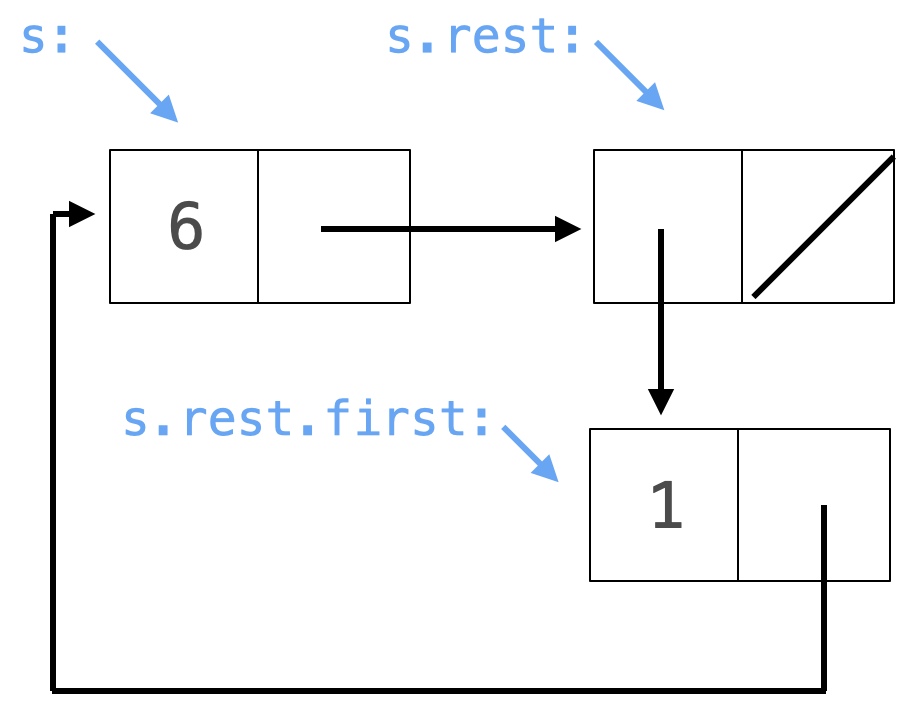
奇怪的循环

创建一个循环需要两个步骤：创建一个没有循环的链表，然后修改它。首先创建，例如，s = Link(6, Link(Link(1)))，然后更改 s.rest.first.rest 以创建循环。

你的答案

在 61A 代码中运行

解决方案

def strange_loop():
    """Return a Link s for which s.rest.first.rest is s.

    >>> s = strange_loop()
    >>> s.rest.first.rest is s
    True
    """
    s = Link(1, Link(Link(2)))
    s.rest.first.rest = s
    return s

Q2: 求和的两种方法

实现 sum_rec 和 sum_iter 两个函数。每个函数都接受一个数字链表 s，并返回其元素的总和。使用递归来实现 sum_rec。不要使用递归来实现 sum_iter；而是使用 while 循环。

引导者： 告诉小组先做哪个。你来决定。你可以说：“咱们先从递归版本开始吧。”

你的答案

在 61A 代码编辑器中运行

答案

def sum_rec(s):
    """
    返回 s 中元素的总和。

    >>> a = Link(1, Link(6, Link(7)))
    >>> sum_rec(a)
    14
    >>> sum_rec(Link.empty)
    0
    """
    # 使用递归调用 sum_rec
    if s == Link.empty:
        return 0
    return s.first + sum_rec(s.rest)

def sum_iter(s):
    """
    返回 s 中元素的总和。

    >>> a = Link(1, Link(6, Link(7)))
    >>> sum_iter(a)
    14
    >>> sum_iter(Link.empty)
    0
    """
    # 不要调用 sum_rec 或 sum_iter
    total = 0
    while s != Link.empty:
        total, s = total + s.first, s.rest
    return total

把 s.first 加到 s.rest 链表剩余元素的总和上。你的基本情况应该判断 s 是否为 Link.empty，这样才能在访问 s.first 或 s.rest 之前确保 s 不为空。

引入一个变量，比如 total，然后在 while 循环里重复执行：把 s.first 加到 total 上，并且让 s = s.rest，以此遍历链表，直到 s 变成 Link.empty 为止。

讨论一下： 加总数字时，中间结果会受到计算顺序的影响。

(1 + 3) + 5 和 1 + (3 + 5) 都等于 9，但第一个在过程中产生 4，而第二个在过程中产生 8。对于同一个链表，sum_rec 和 sum_iter 在过程中产生的中间和是否相同？在你们小组的 Discord 频道文字聊天里回复。如果相同，就发“Same way all day.”。如果不同，就发“Sum thing is different.”

Q3: 交集

实现 overlap 函数，该函数接受两个名为 s 和 t 的数字链表，这两个链表都按递增顺序排序，并且每个链表中都没有重复的元素。它返回两个列表中都出现的数字的计数。

这可以在 s 和 t 的组合长度的线性时间内完成，方法是始终在第一个元素最小的链表中向前推进，直到两个第一个元素相等（将计数加一并同时推进）或一个列表为空（是时候返回了）。这是一个关于此的讲座视频片段（但该视频使用 Python 列表而不是链表）。

投票决定是使用递归还是迭代。无论哪种方式都可以（并且解决方案的复杂性/难度大致相同）。

需要帮助吗？在 Discord 的 #discuss-queue 频道发消息 @discuss over here! 并带上你们的小组号码。

你的答案

在 61A 代码编辑器中运行

答案

def overlap(s, t):
    """对于递增的 s 和 t，计算两个列表中都出现的数字。

    >>> a = Link(3, Link(4, Link(6, Link(7, Link(9, Link(10))))))
    >>> b = Link(1, Link(3, Link(5, Link(7, Link(8)))))
    >>> overlap(a, b)  # 3 和 7
    2
    >>> overlap(a.rest, b)  # 只有 7
    1
    >>> overlap(Link(0, a), Link(0, b))
    3
    """
    if s is Link.empty or t is Link.empty:
        return 0
    if s.first == t.first:
        return 1 + overlap(s.rest, t.rest)
    elif s.first < t.first:
        return overlap(s.rest, t)
    elif s.first > t.first:
        return overlap(s, t.rest)

    if s is Link.empty or t is Link.empty:
        return 0
    if s.first == t.first:
        return __________________
    elif s.first < t.first:
        return __________________
    elif s.first > t.first:
        return __________________

    k = 0
    while s is not Link.empty and t is not Link.empty:
        if s.first == t.first:
            __________________
        elif s.first < t.first:
            __________________
        elif s.first > t.first:
            __________________
    return k

Q4: 重叠增长

``以下是 overlap的另一种实现。假设s和t` 长度相同，那么它的时间复杂度是多少？从下面选项里选一个：常数级别、对数级别、线性级别、平方级别或指数级别。

def length(s):
    if s is Link.empty:
        return 0
    else:
        return 1 + length(s.rest)

def filter_link(f, s):
    if s is Link.empty:
        return s
    else:
        frest = filter_link(f, s.rest)
        if f(s.first):
            return Link(s.first, frest)
        else:
            return frest

def contained_in(s):
    def f(s, x):
        if s is Link.empty:
            return False
        else:
            return s.first == x or f(s.rest, x)
    return lambda x: f(s, x)

def overlap(s, t):
    """For s and t with no repeats, count the numbers that appear in both.

    >>> a = Link(3, Link(4, Link(6, Link(7, Link(9, Link(10))))))
    >>> b = Link(1, Link(3, Link(5, Link(7, Link(8, Link(12))))))
    >>> overlap(a, b)  # 3 and 7
    2
    >>> overlap(a.rest, b.rest)  # just 7
    1
    >>> overlap(Link(0, a), Link(0, b))
    3
    """
    return length(filter_link(contained_in(t), s))

>>> s = Link(0, Link(8, Link(3)))
    >>> s.rest.rest.rest = s.rest.rest
    >>> display(s)
    0.8333333333...
    """
    assert s.first == 0, f'{s.first} is not 0'
    digits = f'{s.first}.'
    s = s.rest
    for _ in range(k):
        assert s.first >= 0 and s.first < 10, f'{s.first} is not a digit'
        digits += str(s.first)
        s = s.rest
    print(digits + '...')

1/22 的十进制展开可以按如下步骤构造：

>>> n, d = 1, 22
>>> n/d
0.045454545454545456
>>> result = Link(0)
>>> tail = result
>>> q, r = 10 * n // d, 10 * n % d
>>> tail.rest = Link(q)  # 得到 0.0
>>> tail = tail.rest
>>> n = r
>>> n
10
>>> q, r = 10 * n // d, 10 * n % d
>>> tail.rest = Link(q)  # 得到 0.04
>>> tail = tail.rest
>>> n = r
>>> n
12
>>> q, r = 10 * n // d, 10 * n % d
>>> tail.rest = Link(q)  # 得到 0.045
>>> tail = tail.rest
>>> n = r
>>> n
10
>>> result
Link(0, Link(0, Link(4, Link(5))))
>>> tail.rest = result.rest.rest
>>> display(result, 20)
0.04545454545454545454...

将上述示例的除法步骤放入 while 循环中：

>>> q, r = 10 * n // d, 10 * n % d
>>> tail.rest = Link(q)
>>> tail = tail.rest
>>> n = r

在构造十进制展开时，将每个 n 对应的 tail 存入以 n 为键的字典。当某个 n 再次出现时，不要创建新的 Link，而是将之前的 Link 的 rest 指向它。这样就形成了一个循环。

Discussion 8 | CS 61A 2024 春季学期

Discussion 8: 链表，效率​

开始​

链表​

Q1：奇怪的循环​

Q2: 求和的两种方法​

Q3: 交集​

Q4: 重叠增长​

Discussion 8: 链表，效率

开始

链表

Q1：奇怪的循环

Q2: 求和的两种方法

Q3: 交集

Q4: 重叠增长